- Uyanan Gençlik forumuna hoşgeldiniz.
Son İletiler
#71
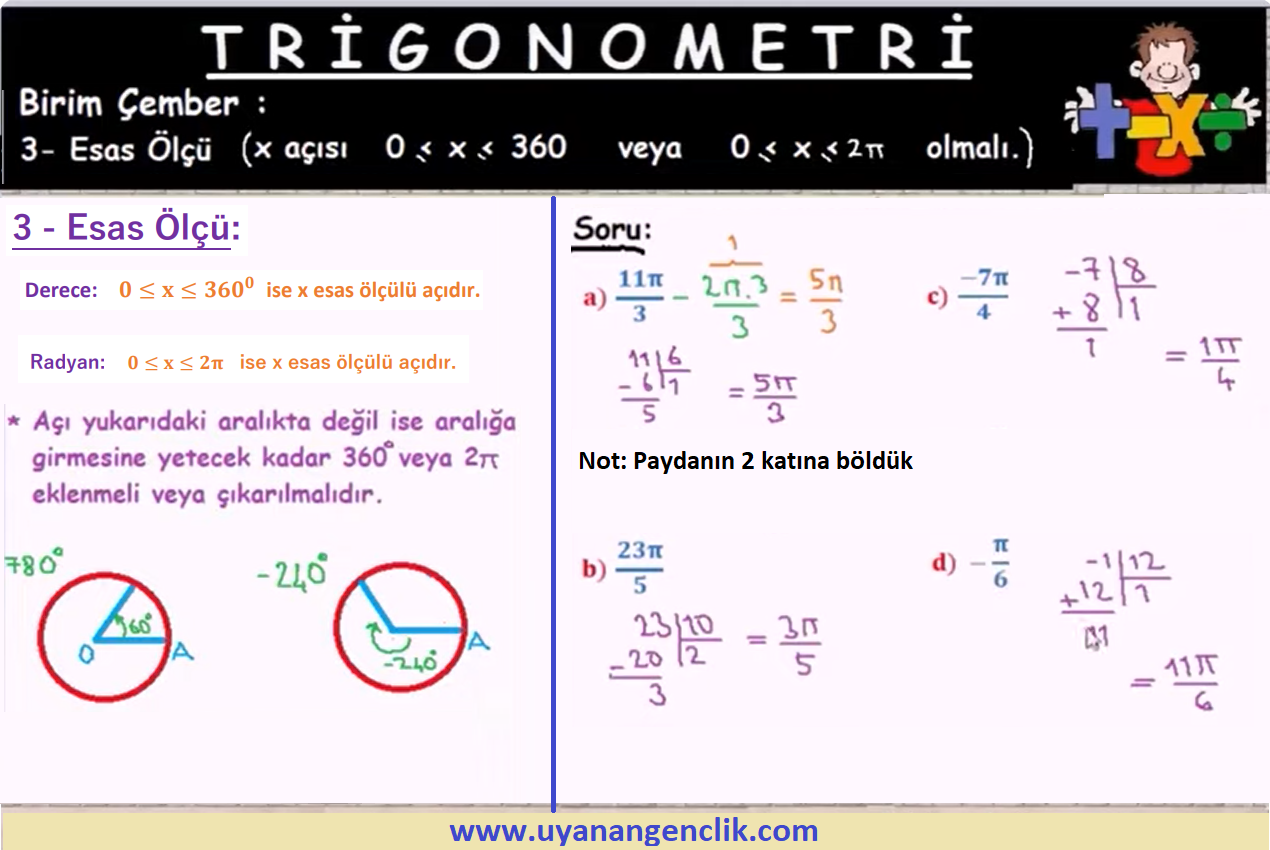
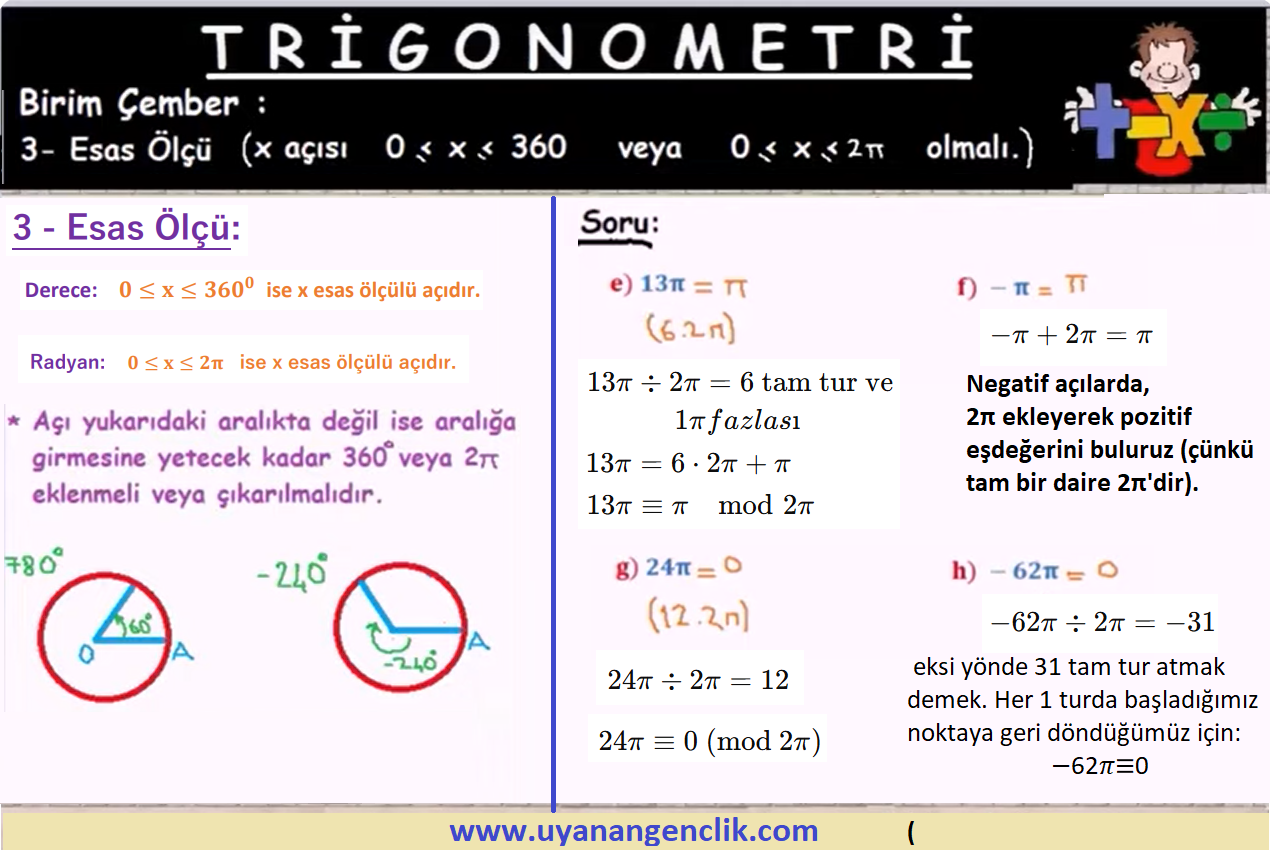
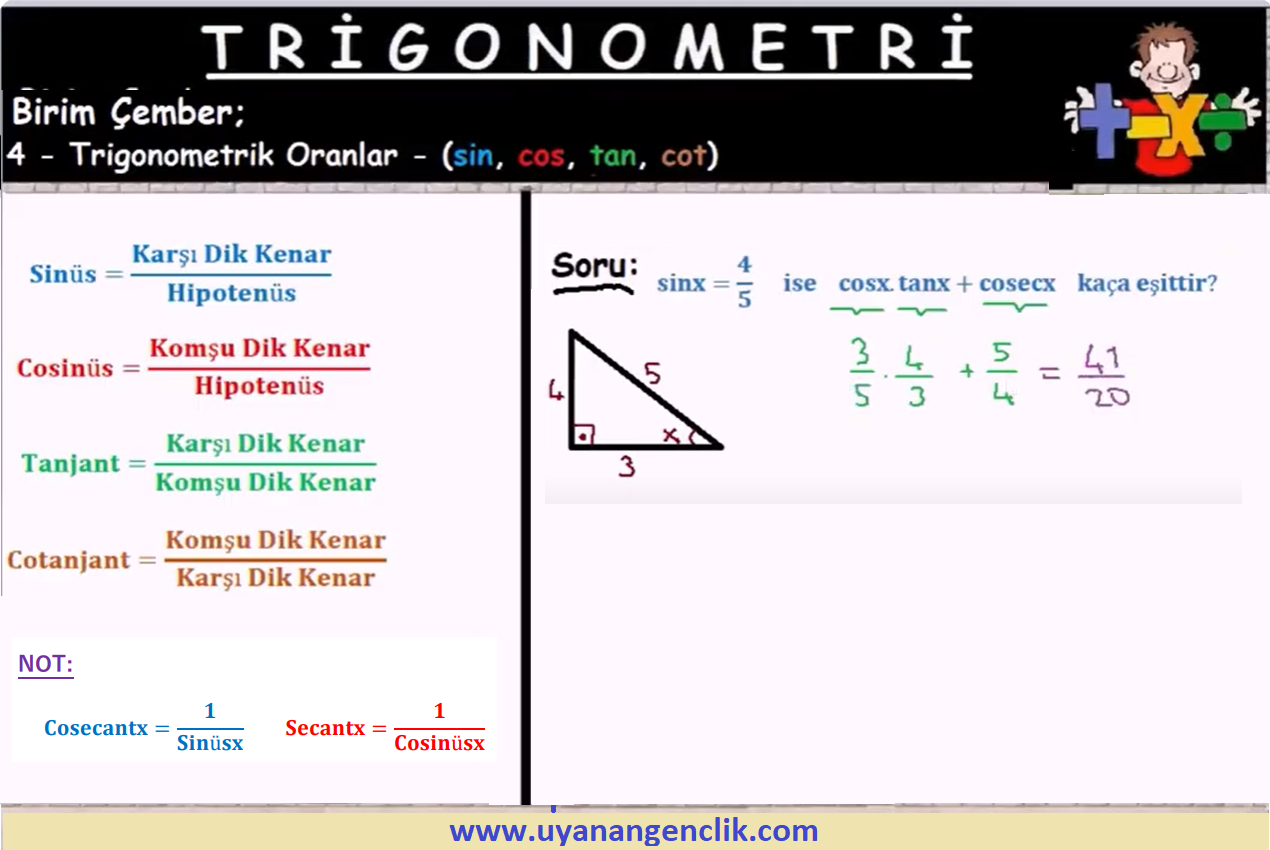
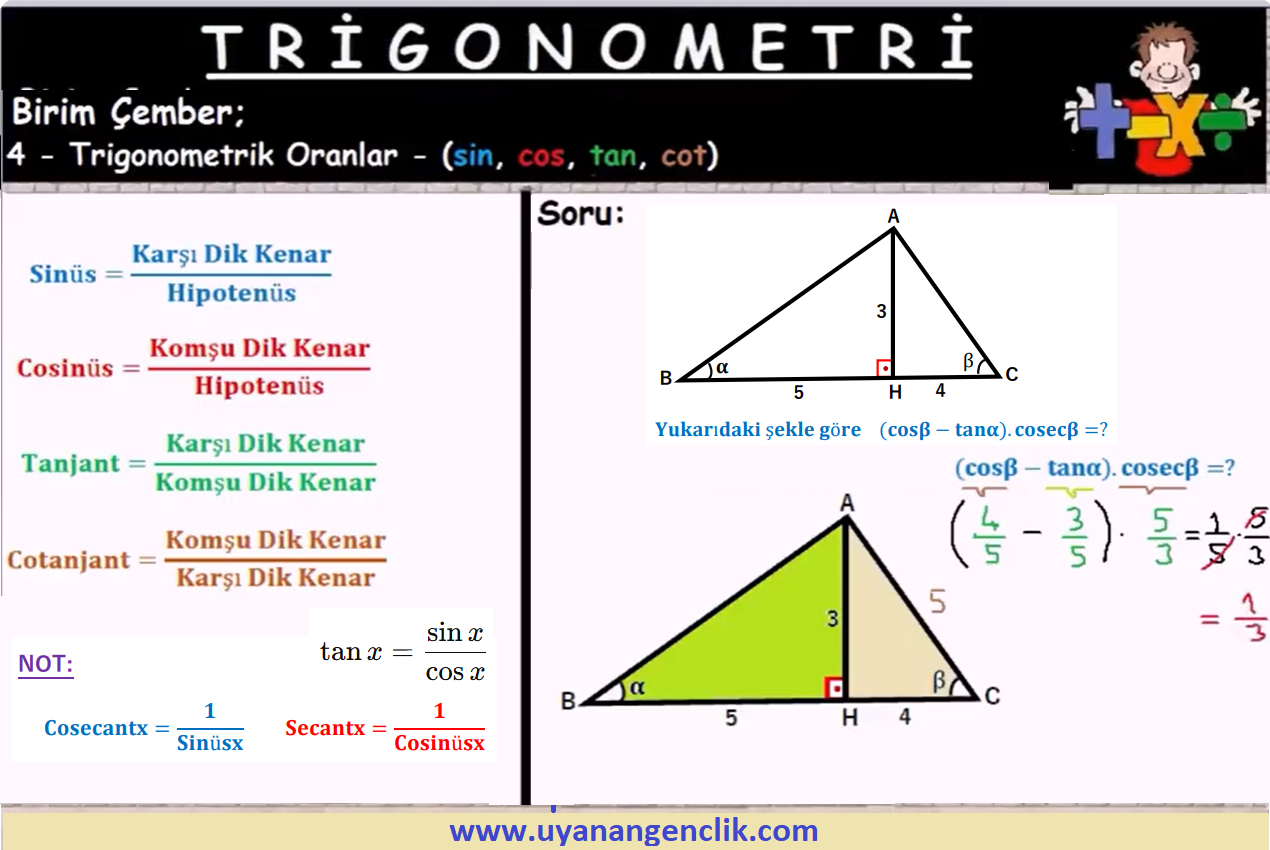
Trigonometri / Trigonometri Soru Çözümleri | ...
Son İleti Gönderen uyanangenclik - Nis 17, 2025, 06:44 ÖÖ









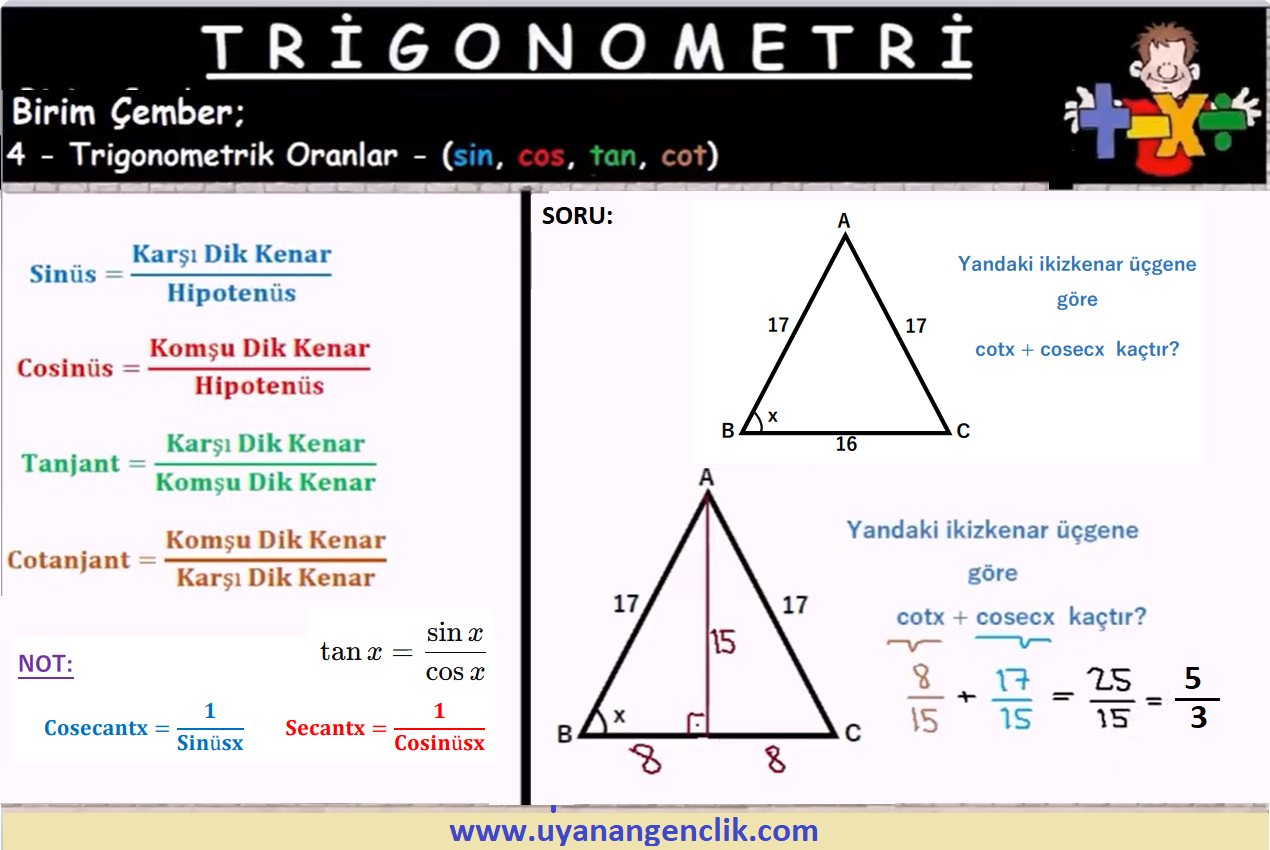
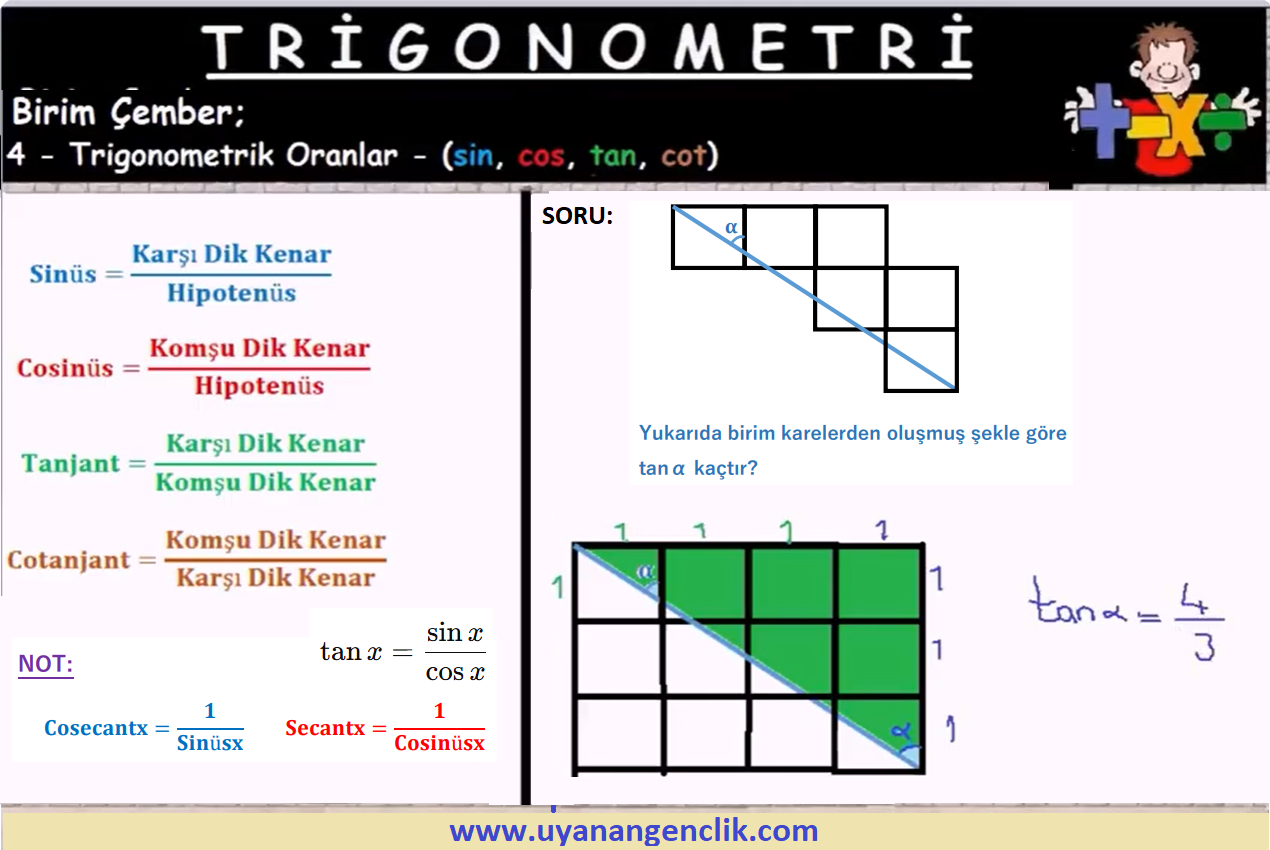


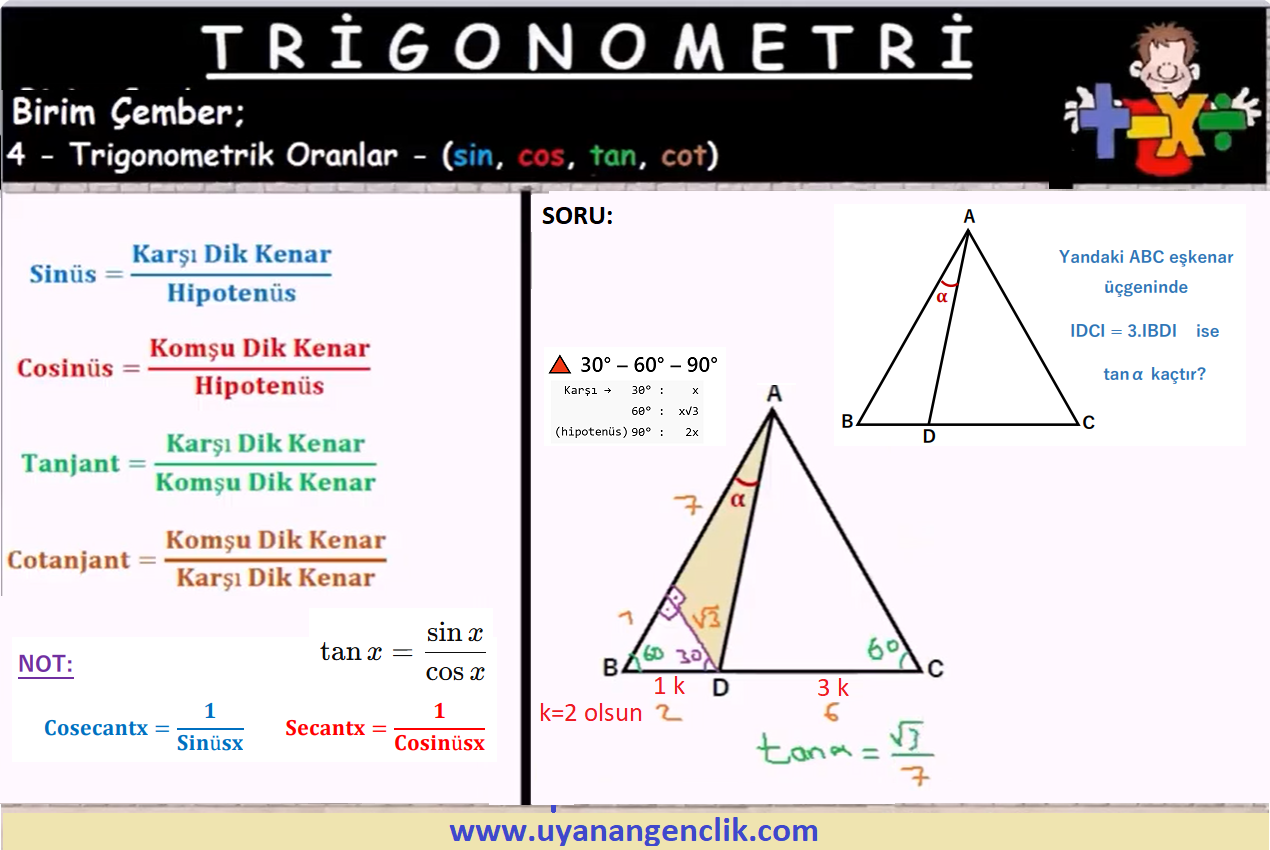


#72
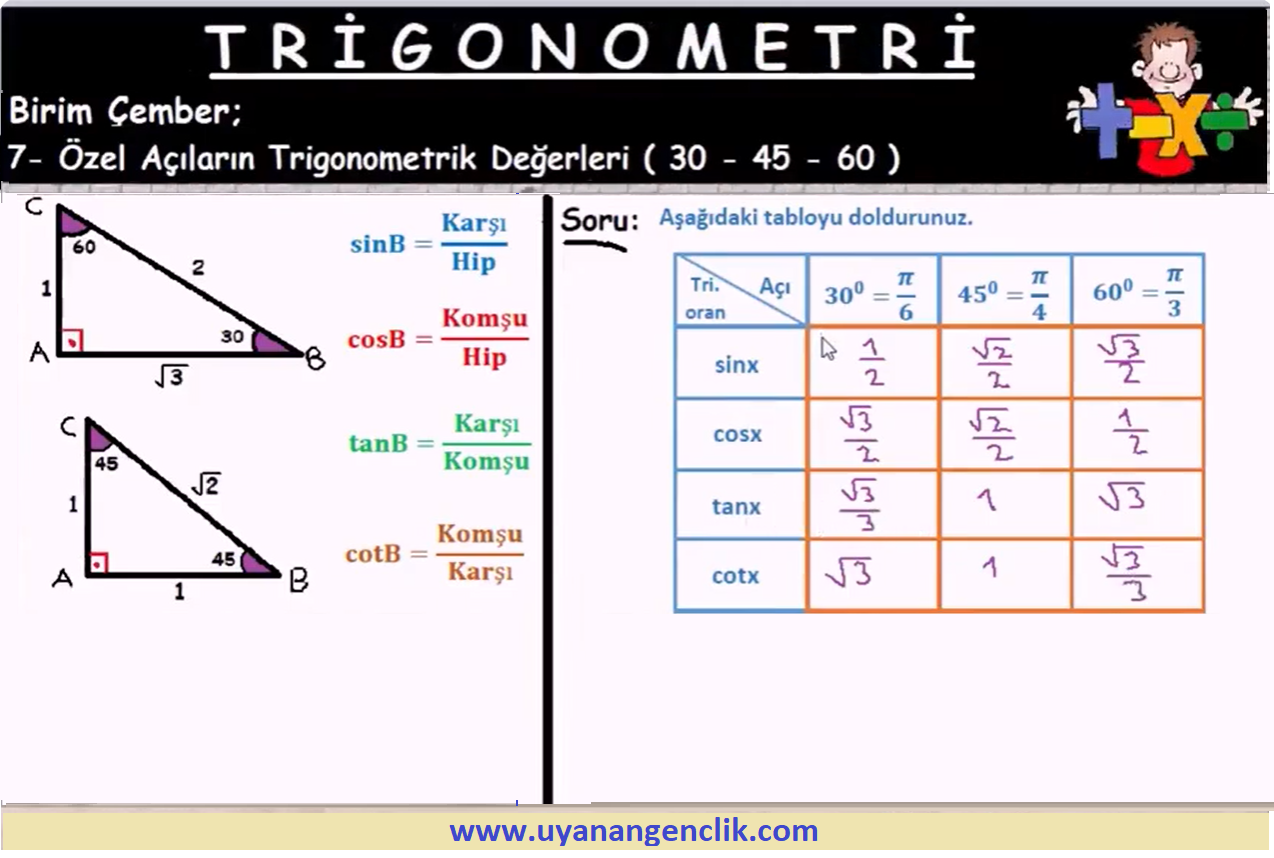
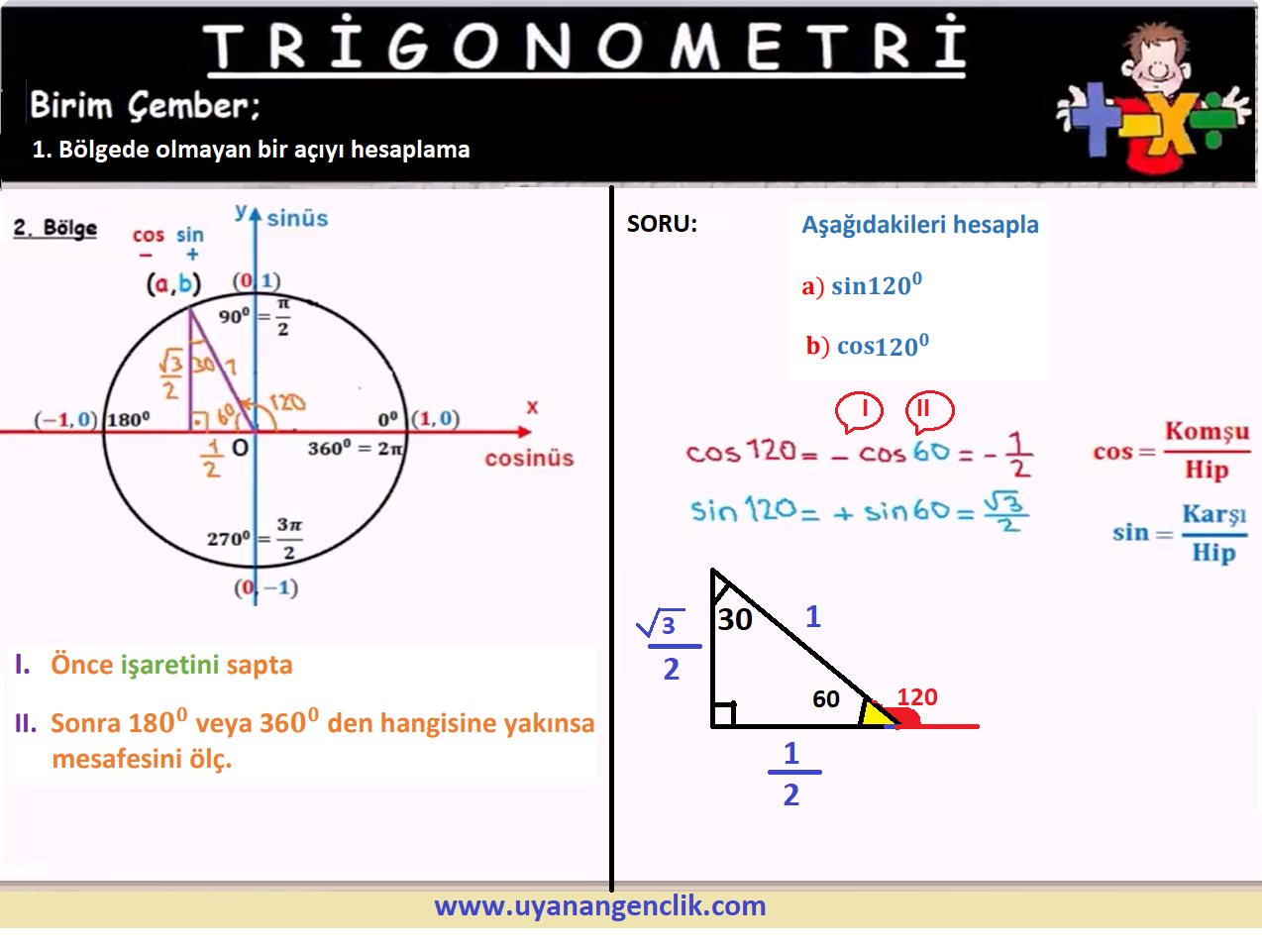
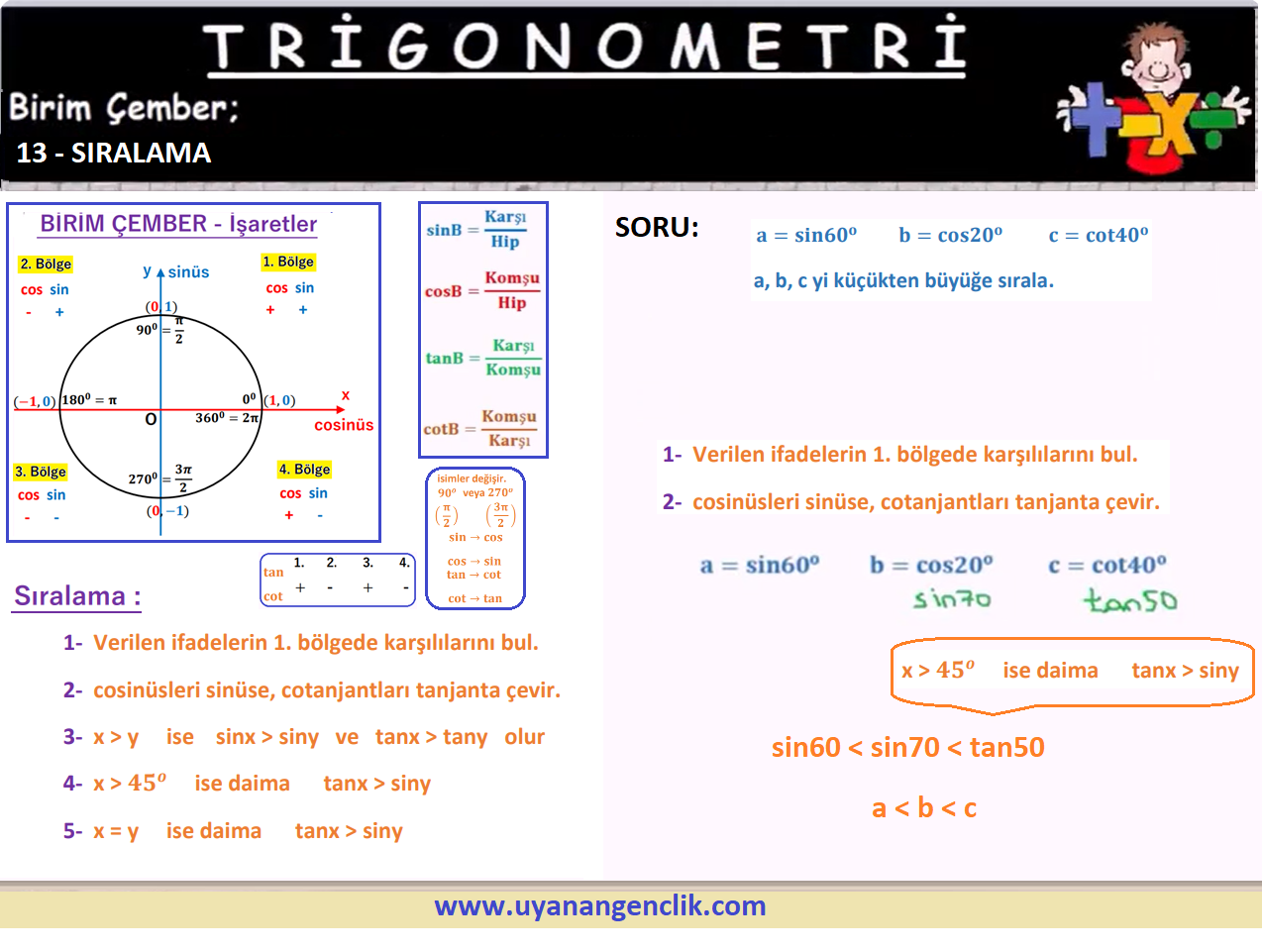
Trigonometri / AYT Trigonometri Konu Anlatım...
Son İleti Gönderen uyanangenclik - Nis 17, 2025, 06:30 ÖÖ





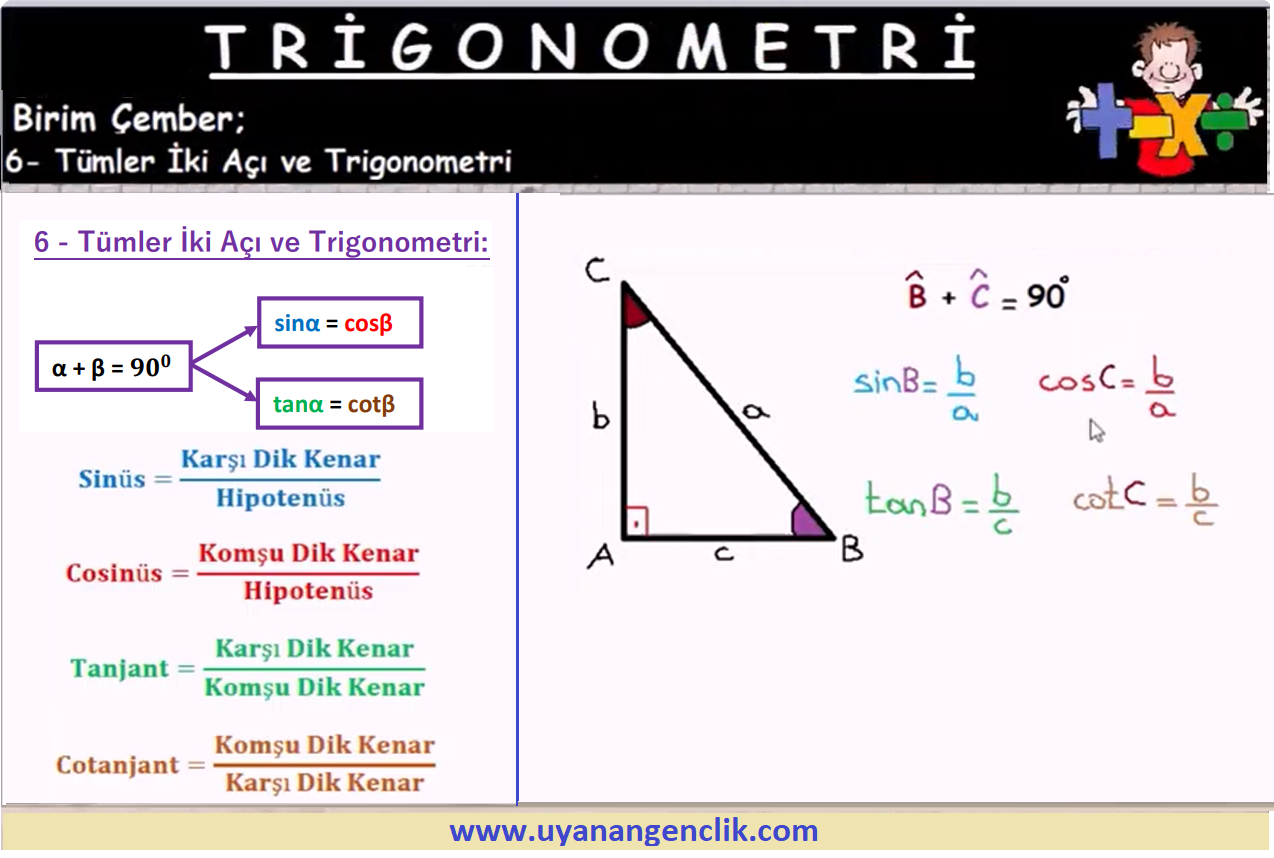



#73
Bulmacalar ve Zeka Oyunları 💡❔ / Sayıları Eşleştirme oyunu
Son İleti Gönderen uyanangenclik - Nis 17, 2025, 06:21 ÖÖSayıları Eşleştirin çizgiler birbirinin üstünden geçmesin.

#74
Logaritma / Logaritma Konu Özeti
Son İleti Gönderen uyanangenclik - Nis 17, 2025, 04:53 ÖÖ📘 LOGARİTMA KONUSU ÖZETİ
📌 Logaritma Nedir?
Bir sayının belli bir tabana göre logaritması, o sayının o tabanın kaçıncı kuvveti olduğunu gösterir.
log_a(b) = x ↔ a^x = b
Burada:
a: taban (a > 0 ve a ≠ 1)
b: logaritması alınan sayı (b > 0)
x: sonuç
📌 Logaritmanın Temel Kuralları:
log_a(1) = 0 → Çünkü a^0 = 1
log_a(a) = 1 → Çünkü a^1 = a
log_a(a^x) = x
a^log_a(x) = x
📌 Logaritma Özellikleri:
1. Çarpma:
log_a(m · n) = log_a(m) + log_a(n)
2. Bölme:
log_a(m / n) = log_a(m) - log_a(n)
3. Üs Alma:
log_a(m^k) = k · log_a(m)
4. Kök Alma:
log_a(√m) = (1/2) · log_a(m)
5. Taban Değiştirme:
log_a(b) = log_c(b) / log_c(a)
En sık kullanılan hali:
log_a(b) = log(b) / log(a)
(Genellikle logaritma tabanı 10 alınır, bu durumda log(x) ifadesi log_10(x) anlamına gelir.)
📌 Özel Logaritmalar:
log_10(x) → Bunu genelde "log x" şeklinde yazarız.
log_e(x) → Bu doğal logaritmadır, "ln x" şeklinde yazılır.
📌 Logaritmanın Tanım Kümesi:
Bir logaritma ifadesinin tanımlı olabilmesi için:
Taban pozitif ve 1'den farklı olmalı → a > 0 ve a ≠ 1
Logaritması alınan ifade pozitif olmalı → b > 0
Örnek:
log_2(x - 3) → tanımlı olması için: x - 3 > 0 → x > 3
📌 Örnekler:
log_2( = ?
= ?
→ 2^3 = 8 → Cevap: 3
log_3(1/9) = ?
→ 3^(-2) = 1/9 → Cevap: -2
log_5(25) = ?
→ 5^2 = 25 → Cevap: 2
📌 Sık Sorulan Logaritma Soruları:
logaritmik ifadelerin sadeleştirilmesi
tanım kümelerinin bulunması
üs ve kök ifadelerinin logaritma içinde kullanılması
eşitlik çözümleri ve logaritma ile çözüm
denklem çözümlerinde log kullanımı
📌 Logaritma Nedir?
Bir sayının belli bir tabana göre logaritması, o sayının o tabanın kaçıncı kuvveti olduğunu gösterir.
log_a(b) = x ↔ a^x = b
Burada:
a: taban (a > 0 ve a ≠ 1)
b: logaritması alınan sayı (b > 0)
x: sonuç
📌 Logaritmanın Temel Kuralları:
log_a(1) = 0 → Çünkü a^0 = 1
log_a(a) = 1 → Çünkü a^1 = a
log_a(a^x) = x
a^log_a(x) = x
📌 Logaritma Özellikleri:
1. Çarpma:
log_a(m · n) = log_a(m) + log_a(n)
2. Bölme:
log_a(m / n) = log_a(m) - log_a(n)
3. Üs Alma:
log_a(m^k) = k · log_a(m)
4. Kök Alma:
log_a(√m) = (1/2) · log_a(m)
5. Taban Değiştirme:
log_a(b) = log_c(b) / log_c(a)
En sık kullanılan hali:
log_a(b) = log(b) / log(a)
(Genellikle logaritma tabanı 10 alınır, bu durumda log(x) ifadesi log_10(x) anlamına gelir.)
📌 Özel Logaritmalar:
log_10(x) → Bunu genelde "log x" şeklinde yazarız.
log_e(x) → Bu doğal logaritmadır, "ln x" şeklinde yazılır.
📌 Logaritmanın Tanım Kümesi:
Bir logaritma ifadesinin tanımlı olabilmesi için:
Taban pozitif ve 1'den farklı olmalı → a > 0 ve a ≠ 1
Logaritması alınan ifade pozitif olmalı → b > 0
Örnek:
log_2(x - 3) → tanımlı olması için: x - 3 > 0 → x > 3
📌 Örnekler:
log_2(
 = ?
= ?→ 2^3 = 8 → Cevap: 3
log_3(1/9) = ?
→ 3^(-2) = 1/9 → Cevap: -2
log_5(25) = ?
→ 5^2 = 25 → Cevap: 2
📌 Sık Sorulan Logaritma Soruları:
logaritmik ifadelerin sadeleştirilmesi
tanım kümelerinin bulunması
üs ve kök ifadelerinin logaritma içinde kullanılması
eşitlik çözümleri ve logaritma ile çözüm
denklem çözümlerinde log kullanımı
#75
Binom / Binom Konu Özeti
Son İleti Gönderen uyanangenclik - Nis 17, 2025, 04:49 ÖÖ📘 BİNOM KONUSU ÖZETİ
Binom Nedir?
Binom, iki terimli ifadelerin (a + b) gibi, n doğal sayısı kadar kuvveti alınarak açılmasıdır. Bu açılım, Binom Açılımı olarak bilinir.
📌 Binom Formülü:
(a + b)^n = C(n,0)·a^n·b^0 + C(n,1)·a^(n-1)·b^1 + ... + C(n,n)·a^0·b^n
Burada:
C(n,r) = Kombinasyon = n! / (r!·(n - r)!)
Terim sayısı: n + 1
En büyük kuvvet a^n ile başlar, b^n ile biter.
📌 Terim Sayısı:
(a + b)^n ifadesinin terim sayısı = n + 1
📌 Binom Açılımında Genel Terim:
T_(r+1) = C(n,r) · a^(n-r) · b^r
Bu formül, (a + b)^n açılımındaki (r+1). terimi verir.
Dikkat! İndisler genellikle 0'dan başladığı için r+1. terim şeklinde yazılır.
📌 Örnek Açılım:
(a + b)^3 =
C(3,0)·a^3·b^0 +
C(3,1)·a^2·b^1 +
C(3,2)·a^1·b^2 +
C(3,3)·a^0·b^3
= 1·a^3 + 3·a^2·b + 3·a·b^2 + 1·b^3
📌 Örnek Soru:
Soru: (2x + 3)^4 ifadesinin açılımında x^2'li terim nedir?
Çözüm:
Genel terim: T_(r+1) = C(4,r) · (2x)^(4−r) · 3^r
x^2'li terim isteniyor → (2x)^(4−r) → x^2 olmalı → 4−r = 2 → r = 2
Şimdi r = 2 için terimi yazalım:
T_3 = C(4,2) · (2x)^2 · 3^2
= 6 · 4x^2 · 9
= 216x^2
📌 Özellikler:
✔ Binom açılımında:
a ve b'nin kuvvetlerinin toplamı her zaman n'dir.
a'nın kuvveti azalır, b'nin kuvveti artar.
Açılımdaki katsayılar Pascal Üçgeni ile de bulunabilir.
📌 Pascal Üçgeni Nedir?
Binom katsayılarının düzenli bir şekilde yazıldığı üçgendir.
n = 0 → 1
n = 1 → 1 1
n = 2 → 1 2 1
n = 3 → 1 3 3 1
n = 4 → 1 4 6 4 1
...
Örnek:
(a + b)^3 → Katsayılar: 1, 3, 3, 1
(a + b)^4 → Katsayılar: 1, 4, 6, 4, 1
📌 Sık Sorulanlar:
Açılımda belirli bir terimi bulma
Belirli bir kuvvetin katsayısını bulma
Sabit terim bulma
Binom katsayıları ile ilgili işlem soruları
Binom Nedir?
Binom, iki terimli ifadelerin (a + b) gibi, n doğal sayısı kadar kuvveti alınarak açılmasıdır. Bu açılım, Binom Açılımı olarak bilinir.
📌 Binom Formülü:
(a + b)^n = C(n,0)·a^n·b^0 + C(n,1)·a^(n-1)·b^1 + ... + C(n,n)·a^0·b^n
Burada:
C(n,r) = Kombinasyon = n! / (r!·(n - r)!)
Terim sayısı: n + 1
En büyük kuvvet a^n ile başlar, b^n ile biter.
📌 Terim Sayısı:
(a + b)^n ifadesinin terim sayısı = n + 1
📌 Binom Açılımında Genel Terim:
T_(r+1) = C(n,r) · a^(n-r) · b^r
Bu formül, (a + b)^n açılımındaki (r+1). terimi verir.
Dikkat! İndisler genellikle 0'dan başladığı için r+1. terim şeklinde yazılır.
📌 Örnek Açılım:
(a + b)^3 =
C(3,0)·a^3·b^0 +
C(3,1)·a^2·b^1 +
C(3,2)·a^1·b^2 +
C(3,3)·a^0·b^3
= 1·a^3 + 3·a^2·b + 3·a·b^2 + 1·b^3
📌 Örnek Soru:
Soru: (2x + 3)^4 ifadesinin açılımında x^2'li terim nedir?
Çözüm:
Genel terim: T_(r+1) = C(4,r) · (2x)^(4−r) · 3^r
x^2'li terim isteniyor → (2x)^(4−r) → x^2 olmalı → 4−r = 2 → r = 2
Şimdi r = 2 için terimi yazalım:
T_3 = C(4,2) · (2x)^2 · 3^2
= 6 · 4x^2 · 9
= 216x^2
📌 Özellikler:
✔ Binom açılımında:
a ve b'nin kuvvetlerinin toplamı her zaman n'dir.
a'nın kuvveti azalır, b'nin kuvveti artar.
Açılımdaki katsayılar Pascal Üçgeni ile de bulunabilir.
📌 Pascal Üçgeni Nedir?
Binom katsayılarının düzenli bir şekilde yazıldığı üçgendir.
n = 0 → 1
n = 1 → 1 1
n = 2 → 1 2 1
n = 3 → 1 3 3 1
n = 4 → 1 4 6 4 1
...
Örnek:
(a + b)^3 → Katsayılar: 1, 3, 3, 1
(a + b)^4 → Katsayılar: 1, 4, 6, 4, 1
📌 Sık Sorulanlar:
Açılımda belirli bir terimi bulma
Belirli bir kuvvetin katsayısını bulma
Sabit terim bulma
Binom katsayıları ile ilgili işlem soruları
#76
Olasılık / Olasılık Konu Özeti
Son İleti Gönderen uyanangenclik - Nis 17, 2025, 04:47 ÖÖ📘 OLASILIK KONUSU ÖZETİ
Olasılık Nedir?
Bir olayın gerçekleşme ihtimalini sayısal olarak ifade eden değerdir.
Olasılık değeri her zaman 0 ile 1 arasındadır.
0 → İmkânsız olay
1 → Kesin olay
Olasılık Formülü:
P(E) = İstenen durum sayısı / Tüm durumların sayısı
P(E): E olayının olma olasılığı
İstenen durum: Soruda bize verilen özel durum
Tüm durum: Olası tüm seçeneklerin toplamı
📌 Olasılık Türleri
Klasik Olasılık:
Tüm sonuçlar eşit olasılıklı ise kullanılır.
Örn: Zar atıldığında 4 gelme olasılığı
Deneysel Olasılık:
Gerçek deneylere dayanarak hesaplanır.
Örn: 100 kez zar atıldı, 6 gelme sayısı 20 ise → 20/100 = 0.2
Öznel Olasılık:
Kişisel tahmin ve yorumlara dayalıdır.
Örn: Bugün yağmur yağma olasılığı yüksek gibi görünüyor.
📌 Sık Kullanılan Olasılık Örnekleri
🎲 Zar Atma:
Bir zar 6 yüzlüdür: 1, 2, 3, 4, 5, 6
3 gelme olasılığı: P(3) = 1 / 6
Tek sayı gelme olasılığı: P(1,3,5) = 3 / 6 = 1 / 2
🃏 Deste Kartlar:
52 kartlık standart deste:
13 kupa, 13 maça, 13 karo, 13 sinek
4 papaz, 4 as, 4 kız...
♦ Kupa gelme olasılığı: 13 / 52 = 1 / 4
♠ Siyah kart gelme olasılığı: 26 / 52 = 1 / 2
🎯 Para Atma:
Yazı gelme olasılığı: 1 / 2
2 para atıldığında her ikisi de tura gelme olasılığı: 1 / 4
📌 Birleşik Olaylar
Ayrık Olaylar:
Birinin gerçekleşmesi diğerini etkilemez.
→ P(A ∪ B) = P(A) + P(B)
Kesişen Olaylar:
Her iki olay aynı anda olabilir.
→ P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
Bağımsız Olaylar:
A ve B olayları birbirinden bağımsız ise:
→ P(A ∩ B) = P(A) × P(B)
📌 Örnekler
Örnek 1:
Bir zar atıldığında 2 gelme olasılığı:
P(2) = 1 / 6
Örnek 2:
Bir deste karttan rastgele bir kart seçiliyor. Papaz gelme olasılığı?
P(Papaz) = 4 / 52 = 1 / 13
Örnek 3:
Bir kutuda 3 kırmızı, 2 mavi top var. Rastgele bir top çekildiğinde kırmızı gelme olasılığı:
P(Kırmızı) = 3 / (3 + 2) = 3 / 5
📌 Olasılıkta Dikkat Edilecek Noktalar:
Olasılık negatif olamaz.
Olasılık 1'den büyük olamaz.
Tüm olası durumları iyi belirlemek önemlidir.
Şans ve olasılık farklı kavramlardır. Olasılık hesaplanabilir, şans subjektiftir.
Olasılık Nedir?
Bir olayın gerçekleşme ihtimalini sayısal olarak ifade eden değerdir.
Olasılık değeri her zaman 0 ile 1 arasındadır.
0 → İmkânsız olay
1 → Kesin olay
Olasılık Formülü:
P(E) = İstenen durum sayısı / Tüm durumların sayısı
P(E): E olayının olma olasılığı
İstenen durum: Soruda bize verilen özel durum
Tüm durum: Olası tüm seçeneklerin toplamı
📌 Olasılık Türleri
Klasik Olasılık:
Tüm sonuçlar eşit olasılıklı ise kullanılır.
Örn: Zar atıldığında 4 gelme olasılığı
Deneysel Olasılık:
Gerçek deneylere dayanarak hesaplanır.
Örn: 100 kez zar atıldı, 6 gelme sayısı 20 ise → 20/100 = 0.2
Öznel Olasılık:
Kişisel tahmin ve yorumlara dayalıdır.
Örn: Bugün yağmur yağma olasılığı yüksek gibi görünüyor.
📌 Sık Kullanılan Olasılık Örnekleri
🎲 Zar Atma:
Bir zar 6 yüzlüdür: 1, 2, 3, 4, 5, 6
3 gelme olasılığı: P(3) = 1 / 6
Tek sayı gelme olasılığı: P(1,3,5) = 3 / 6 = 1 / 2
🃏 Deste Kartlar:
52 kartlık standart deste:
13 kupa, 13 maça, 13 karo, 13 sinek
4 papaz, 4 as, 4 kız...
♦ Kupa gelme olasılığı: 13 / 52 = 1 / 4
♠ Siyah kart gelme olasılığı: 26 / 52 = 1 / 2
🎯 Para Atma:
Yazı gelme olasılığı: 1 / 2
2 para atıldığında her ikisi de tura gelme olasılığı: 1 / 4
📌 Birleşik Olaylar
Ayrık Olaylar:
Birinin gerçekleşmesi diğerini etkilemez.
→ P(A ∪ B) = P(A) + P(B)
Kesişen Olaylar:
Her iki olay aynı anda olabilir.
→ P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
Bağımsız Olaylar:
A ve B olayları birbirinden bağımsız ise:
→ P(A ∩ B) = P(A) × P(B)
📌 Örnekler
Örnek 1:
Bir zar atıldığında 2 gelme olasılığı:
P(2) = 1 / 6
Örnek 2:
Bir deste karttan rastgele bir kart seçiliyor. Papaz gelme olasılığı?
P(Papaz) = 4 / 52 = 1 / 13
Örnek 3:
Bir kutuda 3 kırmızı, 2 mavi top var. Rastgele bir top çekildiğinde kırmızı gelme olasılığı:
P(Kırmızı) = 3 / (3 + 2) = 3 / 5
📌 Olasılıkta Dikkat Edilecek Noktalar:
Olasılık negatif olamaz.
Olasılık 1'den büyük olamaz.
Tüm olası durumları iyi belirlemek önemlidir.
Şans ve olasılık farklı kavramlardır. Olasılık hesaplanabilir, şans subjektiftir.
#77
Kombinasyon / Kombinasyon Konu Özeti
Son İleti Gönderen uyanangenclik - Nis 17, 2025, 04:44 ÖÖ📘 KOMBİNASYON KONUSU ÖZETİ
Kombinasyon Nedir?
Kombinasyon, bir kümeden sırasız olarak eleman seçme işlemidir.
Sıra önemli değildir! Yani, "ABC" ile "CBA" aynı kombinasyondur.
Kombinasyon Formülü:
n elemanlı bir kümeden r tanesini sırasız olarak seçmenin sayısı:
C(n, r) = n! / [r! * (n - r)!]
n! → n faktöriyel
r! → r faktöriyel
(n - r)! → n eksi r'nin faktöriyeli
Kombinasyon Özellikleri:
C(n, r) = C(n, n - r)
(n elemandan r tanesini seçmek ile, geri kalan n−r tanesini seçmek aynı şeydir.)
C(n, 0) = 1 ve C(n, n) = 1
(Bir kümeden hiçbir şey seçmemek veya hepsini seçmek yalnızca 1 şekilde yapılır.)
Kombinasyon Nerelerde Kullanılır?
Loto gibi oyunlarda (Sıra önemli değilse)
Komiteler kurarken
Rastgele grup seçimlerinde
Sırasız takım kurma problemlerinde
📌 Örnekler
Örnek 1:
6 kişilik bir gruptan 2 kişilik bir komite kaç farklı şekilde seçilebilir?
C(6, 2) = 6! / [2! * (6 - 2)!] = (6 × 5) / (2 × 1) = 15
Örnek 2:
10 kitap arasından 3 tanesi okunmak üzere seçilecek. Kaç farklı şekilde seçim yapılabilir?
C(10, 3) = 10! / (3! * 7!) = (10 × 9 × / (3 × 2 × 1) = 120
/ (3 × 2 × 1) = 120
📌 Kombinasyon ile Permütasyon Arasındaki Fark
Özellik Permütasyon Kombinasyon
Sıra Önemli mi? Evet Hayır
Örnek Yarışta 1., 2., 3. belirleme Komite kurma
Formül P(n, r) = n! / (n - r)! C(n, r) = n! / (r!(n - r)!)
📌 Sık Sorulan Kombinasyon Soruları Tipleri
Komite / grup oluşturma
Rastgele seçim problemleri
İsim, sayı, nesne gibi şeylerden belirli sayıda seçme
Seçimlerde "en az", "en fazla" gibi ifadelerle yapılan kombinasyonlar
Sonuç:
Kombinasyonlar, sırasız seçimler için kullanılır.
Permütasyondan farkı sıralamanın önemli olmamasıdır.
Günlük hayattaki seçim problemlerinde oldukça yaygındır.
Kombinasyon Nedir?
Kombinasyon, bir kümeden sırasız olarak eleman seçme işlemidir.
Sıra önemli değildir! Yani, "ABC" ile "CBA" aynı kombinasyondur.
Kombinasyon Formülü:
n elemanlı bir kümeden r tanesini sırasız olarak seçmenin sayısı:
C(n, r) = n! / [r! * (n - r)!]
n! → n faktöriyel
r! → r faktöriyel
(n - r)! → n eksi r'nin faktöriyeli
Kombinasyon Özellikleri:
C(n, r) = C(n, n - r)
(n elemandan r tanesini seçmek ile, geri kalan n−r tanesini seçmek aynı şeydir.)
C(n, 0) = 1 ve C(n, n) = 1
(Bir kümeden hiçbir şey seçmemek veya hepsini seçmek yalnızca 1 şekilde yapılır.)
Kombinasyon Nerelerde Kullanılır?
Loto gibi oyunlarda (Sıra önemli değilse)
Komiteler kurarken
Rastgele grup seçimlerinde
Sırasız takım kurma problemlerinde
📌 Örnekler
Örnek 1:
6 kişilik bir gruptan 2 kişilik bir komite kaç farklı şekilde seçilebilir?
C(6, 2) = 6! / [2! * (6 - 2)!] = (6 × 5) / (2 × 1) = 15
Örnek 2:
10 kitap arasından 3 tanesi okunmak üzere seçilecek. Kaç farklı şekilde seçim yapılabilir?
C(10, 3) = 10! / (3! * 7!) = (10 × 9 ×
 / (3 × 2 × 1) = 120
/ (3 × 2 × 1) = 120📌 Kombinasyon ile Permütasyon Arasındaki Fark
Özellik Permütasyon Kombinasyon
Sıra Önemli mi? Evet Hayır
Örnek Yarışta 1., 2., 3. belirleme Komite kurma
Formül P(n, r) = n! / (n - r)! C(n, r) = n! / (r!(n - r)!)
📌 Sık Sorulan Kombinasyon Soruları Tipleri
Komite / grup oluşturma
Rastgele seçim problemleri
İsim, sayı, nesne gibi şeylerden belirli sayıda seçme
Seçimlerde "en az", "en fazla" gibi ifadelerle yapılan kombinasyonlar
Sonuç:
Kombinasyonlar, sırasız seçimler için kullanılır.
Permütasyondan farkı sıralamanın önemli olmamasıdır.
Günlük hayattaki seçim problemlerinde oldukça yaygındır.
#78
Permütasyon / Permütasyon Konu Özeti
Son İleti Gönderen uyanangenclik - Nis 17, 2025, 04:41 ÖÖ📘 PERMÜTASYON KONUSU ÖZETİ
Permütasyon Nedir?
Permütasyon, bir kümedeki elemanların sıralı dizilişlerini ifade eden bir kavramdır. Başka bir deyişle, belirli bir sayıda elemanın, sırasına dikkat edilerek sıralanması işlemine permütasyon denir. Permütasyonlar, sıralı düzenlemeler olduğu için her sıralama farklı bir düzeni ifade eder.
Permütasyon Formülü:
n elemanlı bir kümeden r eleman seçilip sıralı bir şekilde düzenlendiğinde permütasyon sayısı şu formülle hesaplanır:
P(n, r) = n! / (n - r)!
n! (n faktöriyel), 1'den n'ye kadar olan sayıların çarpımını ifade eder.
(n - r)! ifadesi, seçilen r elemandan geriye kalanların permütasyonunu ifade eder.
Permütasyonun Kullanıldığı Durumlar
Permütasyon, genellikle sıralamanın önemli olduğu durumlarda kullanılır. Örneğin:
Bir yarışta ilk üç sırayı belirlemek.
Bir grup insan arasında liderlik sırasını belirlemek.
Bir etkinlik için yapılacak sıralı yerleştirmeler.
Örnekler
Örnek 1:
5 kişilik bir gruptan 3 kişiyi sıralı bir şekilde seçmek istiyoruz.
Bu durumda permütasyon sayısı şöyle hesaplanır:
P(5, 3) = 5! / (5 - 3)! = 5! / 2! = (5 * 4 * 3) / (1) = 60
Yani, 5 kişiden 3 kişiyi sıralı olarak seçmenin 60 farklı yolu vardır.
Örnek 2:
4 kitap arasında 2 kitabı sırasıyla yerleştirmek istiyoruz.
P(4, 2) = 4! / (4 - 2)! = 4 * 3 = 12
Yani, 4 kitap arasından 2 kitabı sıralı şekilde seçmenin 12 farklı yolu vardır.
Özel Durumlar
Tam Permütasyon (Full Permutation):
Eğer r = n ise, yani tüm elemanlar sıralanacaksa, bu tam permütasyon olarak adlandırılır ve formül şu şekilde olur:
P(n, n) = n!
Yani, n elemanının tüm sıralı düzenlemeleri için permütasyon sayısı n faktöriyel olur.
Tekrarla Permütasyon (Repetition Permutation):
Eğer bazı elemanlar birbirine benzer (tekrarlanan elemanlar varsa), bu durumda tekrarla permütasyon hesaplanır.
Örneğin, "AAB" harflerinden oluşan bir kelimenin sıralamaları hesaplanırken, "A" harfi 2 kez tekrar ettiği için:
P(n1, n2, ..., nk) = n! / (n1! * n2! * ... * nk!)
Burada n, toplam eleman sayısını, n1, n2, ..., nk ise her bir elemanın tekrar sayısını ifade eder.
Permütasyon ile İlgili Sık Sorulan Konular
Permütasyonun Hesaplanması: Permütasyon sayılarının doğru bir şekilde hesaplanması için faktöriyel hesaplamaları yapılır.
Tam Permütasyon vs. Kısmi Permütasyon: Tam permütasyon, tüm elemanların sıralandığı durumdur. Kısmi permütasyon, yalnızca bir kısmının sıralandığı durumdur.
Tekrarla Permütasyon: Aynı öğelerin tekrar ettiği durumlarda, permütasyon hesaplamalarında dikkat edilmesi gereken bir durumdur.
Permütasyonun Pratik Kullanım Alanları: Bir yarışta sıralama yapmak, bir oturma düzeni oluşturmak gibi pratik uygulamalarda permütasyonlar kullanılır.
Permütasyonla İlgili Örnek Sorular
Örnek 1:
7 kişilik bir grup arasında 4 kişiyi sıralı bir şekilde seçmenin kaç farklı yolu vardır?
Cevap:
P(7, 4) = 7! / (7 - 4)! = 7 * 6 * 5 * 4 = 840
Örnek 2:
4 farklı kitap arasından 2'sini sırasıyla yerleştirmenin kaç yolu vardır?
Cevap:
P(4, 2) = 4! / (4 - 2)! = 4 * 3 = 12
Örnek 3:
3 harften "ABA" kelimesinin kaç farklı sıralaması vardır?
Cevap:
P(3, 2, 1) = 3! / 2! = 6 / 2 = 3
Sonuç
Permütasyon, sıralamanın önemli olduğu durumlarda kullanılır ve çeşitli hesaplamalar için temel bir matematiksel araçtır. Özellikle kombinasyonlar, olasılık teorisi ve istatistik gibi alanlarda önemli bir yere sahiptir.
Permütasyon Nedir?
Permütasyon, bir kümedeki elemanların sıralı dizilişlerini ifade eden bir kavramdır. Başka bir deyişle, belirli bir sayıda elemanın, sırasına dikkat edilerek sıralanması işlemine permütasyon denir. Permütasyonlar, sıralı düzenlemeler olduğu için her sıralama farklı bir düzeni ifade eder.
Permütasyon Formülü:
n elemanlı bir kümeden r eleman seçilip sıralı bir şekilde düzenlendiğinde permütasyon sayısı şu formülle hesaplanır:
P(n, r) = n! / (n - r)!
n! (n faktöriyel), 1'den n'ye kadar olan sayıların çarpımını ifade eder.
(n - r)! ifadesi, seçilen r elemandan geriye kalanların permütasyonunu ifade eder.
Permütasyonun Kullanıldığı Durumlar
Permütasyon, genellikle sıralamanın önemli olduğu durumlarda kullanılır. Örneğin:
Bir yarışta ilk üç sırayı belirlemek.
Bir grup insan arasında liderlik sırasını belirlemek.
Bir etkinlik için yapılacak sıralı yerleştirmeler.
Örnekler
Örnek 1:
5 kişilik bir gruptan 3 kişiyi sıralı bir şekilde seçmek istiyoruz.
Bu durumda permütasyon sayısı şöyle hesaplanır:
P(5, 3) = 5! / (5 - 3)! = 5! / 2! = (5 * 4 * 3) / (1) = 60
Yani, 5 kişiden 3 kişiyi sıralı olarak seçmenin 60 farklı yolu vardır.
Örnek 2:
4 kitap arasında 2 kitabı sırasıyla yerleştirmek istiyoruz.
P(4, 2) = 4! / (4 - 2)! = 4 * 3 = 12
Yani, 4 kitap arasından 2 kitabı sıralı şekilde seçmenin 12 farklı yolu vardır.
Özel Durumlar
Tam Permütasyon (Full Permutation):
Eğer r = n ise, yani tüm elemanlar sıralanacaksa, bu tam permütasyon olarak adlandırılır ve formül şu şekilde olur:
P(n, n) = n!
Yani, n elemanının tüm sıralı düzenlemeleri için permütasyon sayısı n faktöriyel olur.
Tekrarla Permütasyon (Repetition Permutation):
Eğer bazı elemanlar birbirine benzer (tekrarlanan elemanlar varsa), bu durumda tekrarla permütasyon hesaplanır.
Örneğin, "AAB" harflerinden oluşan bir kelimenin sıralamaları hesaplanırken, "A" harfi 2 kez tekrar ettiği için:
P(n1, n2, ..., nk) = n! / (n1! * n2! * ... * nk!)
Burada n, toplam eleman sayısını, n1, n2, ..., nk ise her bir elemanın tekrar sayısını ifade eder.
Permütasyon ile İlgili Sık Sorulan Konular
Permütasyonun Hesaplanması: Permütasyon sayılarının doğru bir şekilde hesaplanması için faktöriyel hesaplamaları yapılır.
Tam Permütasyon vs. Kısmi Permütasyon: Tam permütasyon, tüm elemanların sıralandığı durumdur. Kısmi permütasyon, yalnızca bir kısmının sıralandığı durumdur.
Tekrarla Permütasyon: Aynı öğelerin tekrar ettiği durumlarda, permütasyon hesaplamalarında dikkat edilmesi gereken bir durumdur.
Permütasyonun Pratik Kullanım Alanları: Bir yarışta sıralama yapmak, bir oturma düzeni oluşturmak gibi pratik uygulamalarda permütasyonlar kullanılır.
Permütasyonla İlgili Örnek Sorular
Örnek 1:
7 kişilik bir grup arasında 4 kişiyi sıralı bir şekilde seçmenin kaç farklı yolu vardır?
Cevap:
P(7, 4) = 7! / (7 - 4)! = 7 * 6 * 5 * 4 = 840
Örnek 2:
4 farklı kitap arasından 2'sini sırasıyla yerleştirmenin kaç yolu vardır?
Cevap:
P(4, 2) = 4! / (4 - 2)! = 4 * 3 = 12
Örnek 3:
3 harften "ABA" kelimesinin kaç farklı sıralaması vardır?
Cevap:
P(3, 2, 1) = 3! / 2! = 6 / 2 = 3
Sonuç
Permütasyon, sıralamanın önemli olduğu durumlarda kullanılır ve çeşitli hesaplamalar için temel bir matematiksel araçtır. Özellikle kombinasyonlar, olasılık teorisi ve istatistik gibi alanlarda önemli bir yere sahiptir.
#79
Fonksiyonlar / Fonksiyonlar Konu Özeti
Son İleti Gönderen uyanangenclik - Nis 17, 2025, 04:38 ÖÖ📘 FONKSİYONLAR KONUSU ÖZETİ
Fonksiyon Nedir?
Fonksiyon, her bir giriş elemanını (bağımsız değişken) bir çıkış elemanına (bağımlı değişken) eşleyen bir ilişkidir. Yani, bir fonksiyon, bir kümeden diğer bir kümeye elemanları bir kural dahilinde atayan bir yapıdır. Fonksiyonlar genellikle f(x), g(x) gibi sembollerle gösterilir.
Örnek:
Bir fonksiyon olan f, f(x) = 2x + 3 şeklinde olabilir. Burada, x her değer için 2 ile çarpılır ve 3 eklenir.
Fonksiyonun Tanımı
Bir fonksiyon, A kümesinin her elemanını B kümesindeki bir elemana eşler. Yani, her x ∈ A elemanı için, f(x) ∈ B olmalıdır.
Örnek:
Fonksiyon: f(x) = x^2
Eğer A = {-2, -1, 0, 1, 2}, B = {0, 1, 4}, fonksiyonun her bir elemanı şu şekilde eşler:
f(-2) = 4
f(-1) = 1
f(0) = 0
f(1) = 1
f(2) = 4
Fonksiyon Türleri
Birebir Fonksiyon (Injective):
Bir fonksiyon, her x ∈ A değeri için farklı bir f(x) değeri alıyorsa, bu fonksiyon birebirdir. Yani, her giriş için yalnızca bir çıkış vardır.
Örnek:
f(x) = 2x, x ∈ R → Birebirdir.
Üst Üste Binen Fonksiyon (Surjective):
Bir fonksiyon, çıkış kümesinin tüm elemanlarını kapsıyorsa, bu fonksiyon surjectivedir. Başka bir deyişle, f(x) her y ∈ B elemanını kapsar.
Örnek:
f(x) = x^2, x ∈ R → Surjectivedir, çünkü her pozitif sayıya karşılık bir x değeri vardır.
Birebir ve Üst Üste Binen Fonksiyon (Bijective):
Bir fonksiyon, hem birebir hem de üst üste binense, bijektif fonksiyon olarak adlandırılır. Her eleman bir çıkışa karşılık gelir ve her çıkışın bir girişi vardır.
Örnek:
f(x) = x, x ∈ R → Bijektif fonksiyondur.
Fonksiyon Gösterimi
Eşitlik Yöntemi (Fonksiyon Eşitliği):
Fonksiyonlar genellikle eşitlik şeklinde verilir:
f(x) = x + 2 veya f(x) = x^2, g(x) = 3x - 5
Tablo Gösterimi:
Fonksiyonlar, giriş ve çıkış elemanları arasında bir ilişkiyi göstermek için tablolarla ifade edilebilir.
Örnek:
x | -2 | -1 | 0 | 1 | 2
f(x) | 4 | 1 | 0 | 1 | 4
Fonksiyonların Grafiksel Gösterimi
Fonksiyonlar, genellikle bir düzlemde grafikleriyle gösterilir. Bu grafik, x ve y eksenleri üzerinde, giriş (x) ile çıkış (f(x)) arasındaki ilişkiyi görsel olarak ifade eder.
Örnek:
f(x) = x^2 fonksiyonunun grafiği, parabol şeklinde bir eğri oluşturur.
Fonksiyonların Özellikleri
Tanım Kümesi (Domain):
Fonksiyonun girdiği (x) kümesine tanım kümesi denir.
Örnek:
f(x) = 1/x, tanım kümesi, x ≠ 0'dır.
Değer Kümesi (Range):
Fonksiyonun çıktığı (f(x)) kümesine değer kümesi denir.
Örnek:
f(x) = x^2, değer kümesi, f(x) ≥ 0'dır.
Sürekli Fonksiyonlar:
Bir fonksiyon, grafiği üzerinde herhangi bir kesik veya kopma olmadan düzgün bir şekilde çizilebiliyorsa, sürekli fonksiyon olarak kabul edilir.
Fonksiyonun Artan ve Azalanlık Durumu:
Eğer fonksiyon grafiği sağa doğru giderken yükseliyorsa, fonksiyon artandır. Sağdan sola doğru iniş yapıyorsa, fonksiyon azalandır.
Fonksiyonlar ile İlgili Bazı Önemli Kavramlar
Fonksiyonun Ters Fonksiyonu (Inverse Function):
Bir fonksiyonun tersi, giriş ve çıkış elemanlarının yer değiştirilmiş halidir. Bir fonksiyonun tersi yalnızca bijektif fonksiyonlar için tanımlıdır.
Örnek:
f(x) = 2x + 1 → f^(-1)(x) = (x - 1)/2
Kompozisyon (Composition) Fonksiyonları:
İki fonksiyon birleştirilerek tek bir fonksiyon haline getirilebilir. Bu işleme fonksiyonların kompozisyonu denir.
Örnek:
(f ∘ g)(x) = f(g(x))
Örnekler
Örnek 1:
f(x) = x + 3 fonksiyonu verilsin. f(2)'yi bulalım:
f(2) = 2 + 3 = 5
Örnek 2:
g(x) = x^2 fonksiyonu verilsin. g(-3)'ü bulalım:
g(-3) = (-3)^2 = 9
Fonksiyonlar ile İlgili Sık Sorulan Konular
Fonksiyonun tanım kümesi ve değer kümesinin belirlenmesi.
Fonksiyonların artan ve azalanlık özellikleri.
Fonksiyonların tersinin ve kompozisyonunun bulunması.
Grafiklerle fonksiyonun analizi ve belirli noktalar üzerindeki değerlerinin bulunması.
Fonksiyon Nedir?
Fonksiyon, her bir giriş elemanını (bağımsız değişken) bir çıkış elemanına (bağımlı değişken) eşleyen bir ilişkidir. Yani, bir fonksiyon, bir kümeden diğer bir kümeye elemanları bir kural dahilinde atayan bir yapıdır. Fonksiyonlar genellikle f(x), g(x) gibi sembollerle gösterilir.
Örnek:
Bir fonksiyon olan f, f(x) = 2x + 3 şeklinde olabilir. Burada, x her değer için 2 ile çarpılır ve 3 eklenir.
Fonksiyonun Tanımı
Bir fonksiyon, A kümesinin her elemanını B kümesindeki bir elemana eşler. Yani, her x ∈ A elemanı için, f(x) ∈ B olmalıdır.
Örnek:
Fonksiyon: f(x) = x^2
Eğer A = {-2, -1, 0, 1, 2}, B = {0, 1, 4}, fonksiyonun her bir elemanı şu şekilde eşler:
f(-2) = 4
f(-1) = 1
f(0) = 0
f(1) = 1
f(2) = 4
Fonksiyon Türleri
Birebir Fonksiyon (Injective):
Bir fonksiyon, her x ∈ A değeri için farklı bir f(x) değeri alıyorsa, bu fonksiyon birebirdir. Yani, her giriş için yalnızca bir çıkış vardır.
Örnek:
f(x) = 2x, x ∈ R → Birebirdir.
Üst Üste Binen Fonksiyon (Surjective):
Bir fonksiyon, çıkış kümesinin tüm elemanlarını kapsıyorsa, bu fonksiyon surjectivedir. Başka bir deyişle, f(x) her y ∈ B elemanını kapsar.
Örnek:
f(x) = x^2, x ∈ R → Surjectivedir, çünkü her pozitif sayıya karşılık bir x değeri vardır.
Birebir ve Üst Üste Binen Fonksiyon (Bijective):
Bir fonksiyon, hem birebir hem de üst üste binense, bijektif fonksiyon olarak adlandırılır. Her eleman bir çıkışa karşılık gelir ve her çıkışın bir girişi vardır.
Örnek:
f(x) = x, x ∈ R → Bijektif fonksiyondur.
Fonksiyon Gösterimi
Eşitlik Yöntemi (Fonksiyon Eşitliği):
Fonksiyonlar genellikle eşitlik şeklinde verilir:
f(x) = x + 2 veya f(x) = x^2, g(x) = 3x - 5
Tablo Gösterimi:
Fonksiyonlar, giriş ve çıkış elemanları arasında bir ilişkiyi göstermek için tablolarla ifade edilebilir.
Örnek:
x | -2 | -1 | 0 | 1 | 2
f(x) | 4 | 1 | 0 | 1 | 4
Fonksiyonların Grafiksel Gösterimi
Fonksiyonlar, genellikle bir düzlemde grafikleriyle gösterilir. Bu grafik, x ve y eksenleri üzerinde, giriş (x) ile çıkış (f(x)) arasındaki ilişkiyi görsel olarak ifade eder.
Örnek:
f(x) = x^2 fonksiyonunun grafiği, parabol şeklinde bir eğri oluşturur.
Fonksiyonların Özellikleri
Tanım Kümesi (Domain):
Fonksiyonun girdiği (x) kümesine tanım kümesi denir.
Örnek:
f(x) = 1/x, tanım kümesi, x ≠ 0'dır.
Değer Kümesi (Range):
Fonksiyonun çıktığı (f(x)) kümesine değer kümesi denir.
Örnek:
f(x) = x^2, değer kümesi, f(x) ≥ 0'dır.
Sürekli Fonksiyonlar:
Bir fonksiyon, grafiği üzerinde herhangi bir kesik veya kopma olmadan düzgün bir şekilde çizilebiliyorsa, sürekli fonksiyon olarak kabul edilir.
Fonksiyonun Artan ve Azalanlık Durumu:
Eğer fonksiyon grafiği sağa doğru giderken yükseliyorsa, fonksiyon artandır. Sağdan sola doğru iniş yapıyorsa, fonksiyon azalandır.
Fonksiyonlar ile İlgili Bazı Önemli Kavramlar
Fonksiyonun Ters Fonksiyonu (Inverse Function):
Bir fonksiyonun tersi, giriş ve çıkış elemanlarının yer değiştirilmiş halidir. Bir fonksiyonun tersi yalnızca bijektif fonksiyonlar için tanımlıdır.
Örnek:
f(x) = 2x + 1 → f^(-1)(x) = (x - 1)/2
Kompozisyon (Composition) Fonksiyonları:
İki fonksiyon birleştirilerek tek bir fonksiyon haline getirilebilir. Bu işleme fonksiyonların kompozisyonu denir.
Örnek:
(f ∘ g)(x) = f(g(x))
Örnekler
Örnek 1:
f(x) = x + 3 fonksiyonu verilsin. f(2)'yi bulalım:
f(2) = 2 + 3 = 5
Örnek 2:
g(x) = x^2 fonksiyonu verilsin. g(-3)'ü bulalım:
g(-3) = (-3)^2 = 9
Fonksiyonlar ile İlgili Sık Sorulan Konular
Fonksiyonun tanım kümesi ve değer kümesinin belirlenmesi.
Fonksiyonların artan ve azalanlık özellikleri.
Fonksiyonların tersinin ve kompozisyonunun bulunması.
Grafiklerle fonksiyonun analizi ve belirli noktalar üzerindeki değerlerinin bulunması.
#80
Kümeler / Kümeler Konu Özeti
Son İleti Gönderen uyanangenclik - Nis 17, 2025, 04:37 ÖÖ📘 KÜMELER KONUSU ÖZETİ
Küme Nedir?
Küme, belirli bir özelliğe sahip elemanların bir araya getirilmesiyle oluşan bir topluluktur. Matematiksel olarak, bir küme, belirli öğelerin (elemanların) bir araya gelmesiyle oluşturulan bir yapıdır. Bir küme, sıklıkla büyük harflerle (A, B, C gibi) gösterilir ve elemanlar süslü parantezler {} içerisinde belirtilir.
Örnek:
A = {1, 2, 3, 4} → A kümesi, 1, 2, 3, 4 sayılarından oluşur.
Küme Gösterimi
Liste Yöntemi (Element Yöntemi):
Bir küme, elemanları sıralayarak veya belirterek gösterilir.
Örnek:
A = {1, 2, 3, 4}
Varlık Yöntemi (Özellik Yöntemi):
Elemanları tek tek yazmak yerine, kümeye ait özellik belirtilerek de küme gösterilebilir.
Örnek:
A = {x | x ∈ Z, x < 5} → 5'ten küçük tüm tam sayılardan oluşan küme.
Küme Türleri
Boş Küme (Null Set):
Hiçbir elemanı olmayan küme, boş küme olarak adlandırılır ve {} veya ∅ ile gösterilir.
Örnek:
B = {} veya B = ∅
Sonlu Küme:
Eleman sayısı belirli olan küme sonlu küme olarak adlandırılır.
Örnek:
C = {a, b, c}
Sonsuz Küme:
Eleman sayısı sonsuz olan kümelere sonsuz küme denir.
Örnek:
D = {1, 2, 3, 4, ...} → Doğal sayılar kümesi.
Evrensel Küme (U):
Bir problemde ele alınan tüm elemanların yer aldığı küme evrensel kümedir. Evrensel küme, genellikle U harfiyle gösterilir.
Örnek:
U = {tüm insanlar}
Alt Küme (Subset):
Bir kümenin her elemanı başka bir kümenin elemanlarıysa, o küme alt küme olarak adlandırılır.
Örnek:
A = {1, 2}, B = {1, 2, 3} → A, B'nin alt kümesidir.
Kendi Kendine Alt Küme (Improper Subset):
Bir küme, kendisinin de alt kümesi olabilir.
Örnek:
A = {1, 2, 3} → A, kendisinin alt kümesidir.
Kesin Alt Küme (Proper Subset):
Bir küme, başka bir kümenin alt kümesi olabilir, ancak kendisini içermeyen bir alt küme olarak kabul edilir.
Örnek:
A = {1, 2}, B = {1, 2, 3} → A, B'nin kesin alt kümesidir.
Kümelerde İşlemler
Birleşim (Union):
İki kümenin birleşimi, her iki kümenin elemanlarının bir araya getirilmesidir. Birleşim, ∪ sembolü ile gösterilir.
Örnek:
A = {1, 2, 3}, B = {3, 4, 5}
A ∪ B = {1, 2, 3, 4, 5}
Kesişim (Intersection):
İki kümenin kesişimi, her iki kümede de bulunan ortak elemanlardan oluşur. Kesişim, ∩ sembolü ile gösterilir.
Örnek:
A = {1, 2, 3}, B = {3, 4, 5}
A ∩ B = {3}
Fark (Difference):
A kümesinin B kümesinden farkı, A kümesindeki elemanlardan B kümesindeki elemanların çıkarılmasıyla oluşur. Fark, − sembolü ile gösterilir.
Örnek:
A = {1, 2, 3}, B = {3, 4, 5}
A − B = {1, 2}
Simetrik Fark (Symmetric Difference):
İki kümenin simetrik farkı, her iki kümede olup diğerinde olmayan elemanlardan oluşur. Simetrik fark, Δ sembolü ile gösterilir.
Örnek:
A = {1, 2, 3}, B = {3, 4, 5}
A Δ B = {1, 2, 4, 5}
Kümelerin Kartesyen Çarpımı (Cartesian Product):
İki kümenin kartesyen çarpımı, bir küme elemanları ile diğer küme elemanlarının tüm olası sıralı çiftlerini içerir. Kartesyen çarpım, × sembolü ile gösterilir.
Örnek:
A = {1, 2}, B = {x, y}
A × B = {(1, x), (1, y), (2, x), (2, y)}
Küme İlişkileri
Eşitlik:
İki küme, tıpkı birbirlerinin elemanlarına sahipse eşittir.
Örnek:
A = {1, 2, 3}, B = {1, 2, 3} → A = B
Alt Küme İlişkisi:
Bir küme, diğer kümenin alt kümesi olabilir.
Farklılık:
İki küme, hiçbir ortak elemanı paylaşmıyorsa farklıdır. Bu durum "boş kesişim" anlamına gelir.
Örnek:
A = {1, 2, 3}, B = {4, 5, 6} → A ∩ B = ∅
ÖZET
Küme, belirli elemanlardan oluşan bir topluluktur ve matematiksel işlemlerin temelini oluşturur. Küme türleri ve küme işlemleri, daha karmaşık matematiksel kavramların anlaşılması için önemlidir. Küme teorisi, mantık, fonksiyonlar, sayı teorisi gibi birçok matematiksel alanın temelini atar ve her biri farklı problemlerin çözülmesinde kritik rol oynar.
Küme Nedir?
Küme, belirli bir özelliğe sahip elemanların bir araya getirilmesiyle oluşan bir topluluktur. Matematiksel olarak, bir küme, belirli öğelerin (elemanların) bir araya gelmesiyle oluşturulan bir yapıdır. Bir küme, sıklıkla büyük harflerle (A, B, C gibi) gösterilir ve elemanlar süslü parantezler {} içerisinde belirtilir.
Örnek:
A = {1, 2, 3, 4} → A kümesi, 1, 2, 3, 4 sayılarından oluşur.
Küme Gösterimi
Liste Yöntemi (Element Yöntemi):
Bir küme, elemanları sıralayarak veya belirterek gösterilir.
Örnek:
A = {1, 2, 3, 4}
Varlık Yöntemi (Özellik Yöntemi):
Elemanları tek tek yazmak yerine, kümeye ait özellik belirtilerek de küme gösterilebilir.
Örnek:
A = {x | x ∈ Z, x < 5} → 5'ten küçük tüm tam sayılardan oluşan küme.
Küme Türleri
Boş Küme (Null Set):
Hiçbir elemanı olmayan küme, boş küme olarak adlandırılır ve {} veya ∅ ile gösterilir.
Örnek:
B = {} veya B = ∅
Sonlu Küme:
Eleman sayısı belirli olan küme sonlu küme olarak adlandırılır.
Örnek:
C = {a, b, c}
Sonsuz Küme:
Eleman sayısı sonsuz olan kümelere sonsuz küme denir.
Örnek:
D = {1, 2, 3, 4, ...} → Doğal sayılar kümesi.
Evrensel Küme (U):
Bir problemde ele alınan tüm elemanların yer aldığı küme evrensel kümedir. Evrensel küme, genellikle U harfiyle gösterilir.
Örnek:
U = {tüm insanlar}
Alt Küme (Subset):
Bir kümenin her elemanı başka bir kümenin elemanlarıysa, o küme alt küme olarak adlandırılır.
Örnek:
A = {1, 2}, B = {1, 2, 3} → A, B'nin alt kümesidir.
Kendi Kendine Alt Küme (Improper Subset):
Bir küme, kendisinin de alt kümesi olabilir.
Örnek:
A = {1, 2, 3} → A, kendisinin alt kümesidir.
Kesin Alt Küme (Proper Subset):
Bir küme, başka bir kümenin alt kümesi olabilir, ancak kendisini içermeyen bir alt küme olarak kabul edilir.
Örnek:
A = {1, 2}, B = {1, 2, 3} → A, B'nin kesin alt kümesidir.
Kümelerde İşlemler
Birleşim (Union):
İki kümenin birleşimi, her iki kümenin elemanlarının bir araya getirilmesidir. Birleşim, ∪ sembolü ile gösterilir.
Örnek:
A = {1, 2, 3}, B = {3, 4, 5}
A ∪ B = {1, 2, 3, 4, 5}
Kesişim (Intersection):
İki kümenin kesişimi, her iki kümede de bulunan ortak elemanlardan oluşur. Kesişim, ∩ sembolü ile gösterilir.
Örnek:
A = {1, 2, 3}, B = {3, 4, 5}
A ∩ B = {3}
Fark (Difference):
A kümesinin B kümesinden farkı, A kümesindeki elemanlardan B kümesindeki elemanların çıkarılmasıyla oluşur. Fark, − sembolü ile gösterilir.
Örnek:
A = {1, 2, 3}, B = {3, 4, 5}
A − B = {1, 2}
Simetrik Fark (Symmetric Difference):
İki kümenin simetrik farkı, her iki kümede olup diğerinde olmayan elemanlardan oluşur. Simetrik fark, Δ sembolü ile gösterilir.
Örnek:
A = {1, 2, 3}, B = {3, 4, 5}
A Δ B = {1, 2, 4, 5}
Kümelerin Kartesyen Çarpımı (Cartesian Product):
İki kümenin kartesyen çarpımı, bir küme elemanları ile diğer küme elemanlarının tüm olası sıralı çiftlerini içerir. Kartesyen çarpım, × sembolü ile gösterilir.
Örnek:
A = {1, 2}, B = {x, y}
A × B = {(1, x), (1, y), (2, x), (2, y)}
Küme İlişkileri
Eşitlik:
İki küme, tıpkı birbirlerinin elemanlarına sahipse eşittir.
Örnek:
A = {1, 2, 3}, B = {1, 2, 3} → A = B
Alt Küme İlişkisi:
Bir küme, diğer kümenin alt kümesi olabilir.
Farklılık:
İki küme, hiçbir ortak elemanı paylaşmıyorsa farklıdır. Bu durum "boş kesişim" anlamına gelir.
Örnek:
A = {1, 2, 3}, B = {4, 5, 6} → A ∩ B = ∅
ÖZET
Küme, belirli elemanlardan oluşan bir topluluktur ve matematiksel işlemlerin temelini oluşturur. Küme türleri ve küme işlemleri, daha karmaşık matematiksel kavramların anlaşılması için önemlidir. Küme teorisi, mantık, fonksiyonlar, sayı teorisi gibi birçok matematiksel alanın temelini atar ve her biri farklı problemlerin çözülmesinde kritik rol oynar.

