Denklem Kurma Problemleri Örnek:
Bir sayının 2 eksiğinin 3 katı 15’dir. Bu sayı kaçtır?
ÇÖZÜM:
(x-2).3=15
Her iki tarafı 3’e böleriz
x-2=5 olur.-2 diğer tarafa +2 geçer.
x=5+2
=7
Örnek:
Bir sayının 3 katının 2 eksiği 13’tür. Bu sayı kaçtır?
ÇÖZÜM:
3.x-2=13
-2 diğer tarafa +2 geçer.
3x=13+2
3x=15 her iki taraf 3’e bölünür.
x=5
Örnek:
Bir sayının 2 katının 4 fazlası 26 ise, bu sayı kaçtır?
ÇÖZÜM:
Sayımız x olsun.
2 katı → 2x
2 katının 4 fazlası → 2x + 4 olur.
Denklemimiz ise;
2x + 4 = 26
2x = 26 - 4
2x = 22
x = 11 olur.
Örnek:
Biri diğerinden 5 fazla olan iki doğal sayının toplamı 77 olduğuna göre, küçük sayı kaçtır?
ÇÖZÜM:
Küçük sayı x ise diğer sayı x+5 olur.
Toplamları 77 olduğuna göre;
x + x + 5 = 77
2x + 5 = 77
2x = 77 - 5
2x = 72
x = 36 olur.
Örnek:
İki sayının toplamı 217'dir. Büyük sayı küçük sayının 6 katı olduğuna göre büyük sayı kaçtır?
ÇÖZÜM:
Küçük sayı → x
Büyük sayı → 6x
Toplamları 217 olduğuna göre;
x + 6x = 217
7x = 217
x = 31 olur.
Büyük sayı ise;
6x = 6 . 31 = 186 olur.
Örnek:
İki sayının toplamı 78, farkları ise 48'dir. Büyük sayı kaçtır?
ÇÖZÜM:
Küçük sayı → x
Büyük sayı → x+48 (Farkları 48 olduğu için büyük sayı küçük sayıdan 48 fazladır.)
Bu iki sayının toplamı 78 ise;
x + x + 48 = 78
2x + 48 = 78
2x = 78 − 48
2x = 30
x = 15 (küçük sayı)
Büyük sayı ise 15 + 48 = 63 tür.
Örnek:
Hangi sayının 3 katının 20 eksiği kendisine eşittir?
ÇÖZÜM:
Sayımız x olsun.
3 katı → 3x
3 katının 20 eksiği → 3x − 20
Bu ifade kendisine eşit olduğuna göre;
3x − 20 = x
3x − x = 20
2x = 20
x = 10
Örnek:
Bir sayının 4 fazlasının 3 katı 87 ise bu sayı kaçtır?
ÇÖZÜM:
Sayımız x olsun.
4 fazlası → x+4
4 fazlasının 3 katı → 3.(x+4)
Şimdi denklemimizi yazalım.
3.(x+4) = 87
3x + 12 = 87
3x = 87 − 12
3x = 75
x = 25
Örnek:
Bir baba ile oğlunun yaşları toplamı 48'dir. Babanın yaşı oğlunun yaşının 3 katından 4 fazla ise baba kaç yaşındadır?
ÇÖZÜM:
Oğlu → x
Baba → 3x + 4
Yaşları toplamı 48 olduğuna göre;
x + 3x + 4 = 48
4x + 4 = 48
4x = 48 − 4
4x = 44
x = 11 (Çocuk)
Baba ise, 3 . 11 + 4 = 37 yaşındadır.
Örnek:
Yavuz ve Hasan 300 TL'yi paylaşıyorlar. Yavuz, Hasan'ın 2 katından 60 TL fazla alıyor. Hasan kaç TL alır?
ÇÖZÜM:
Hasan'ın parası → x
Yavuz'un parası → 2x + 60
Paraları toplamı 300 TL olduğu için;
x + 2x + 60 = 300
3x + 60 = 300
3x = 300 − 60
3x = 240
x = 80 TL (Hasan)
Örnek:
Toplamları 146 olan iki sayıdan biri diğerinden 14 eksiktir. Küçük sayı kaçtır?
ÇÖZÜM:
Büyük sayı → x
Küçük sayı → x − 14
Toplamları 146 olduğuna göre;
x + x − 14 = 146
2x − 14 = 146
2x = 146 + 14
2x = 160
x = 80 (Büyük sayı)
Küçük sayı ise; 80 − 14 = 66 olur.
Örnek:
Hakan 22, Zehra 10 yaşındadır. Kaç yıl önce, Hakan'ın yaşı Zehra'nın yaşının 3 katıdır?
ÇÖZÜM:
x yıl önce Hakan (22 − x) yaşında,
x yıl önce Zehra (10 − x) yaşındadır.
x yıl önce Hakan'ın yaşı Zehra'nın yaşının 3 katı ise;
(22 − x) = 3.(10 − x)
22 − x = 30 − 3x
3x − x = 30 − 22
2x = 8
x = 4
Örnek:
178 cevizi üç kardeş paylaşıyor. Ortanca küçükten 10 fazla, büyükten 8 eksik alıyor. Ortanca kardeş kaç ceviz almıştır?
ÇÖZÜM:
Küçük kardeş → x
Ortanca kardeş → (x + 10)
Büyük kardeş (x + 18) (Ortanca büyükten 8 eksik aldığına göre, büyük ortancadan 8 fazla almıştır)
Toplam 178 ceviz olduğuna göre;
x + (x + 10) + (x + 18) = 178
3x + 28 = 178
3x = 178 − 28
3x = 150
x = 50 (küçük kardeş)
Ortanca ise 50 + 10 = 60 ceviz alır.
Örnek:
Fırat'ın parasının 8 TL eksiği ile 14 TL fazlasının toplamı 128 TL olduğuna göre Fırat'ın kaç TL'si vardır?
ÇÖZÜM:
Fırat'ın parası x TL olsun.
8 TL eksiği → (x − 8) TL
14 TL fazlası → (x + 14) TL
Toplamları 128 TL olduğu için;
(x − 8) + (x + 14) = 128
2x + 6 = 128
2x = 128 − 6
2x = 122
x = 61 TL
Örnek:
Ardışık üç çift doğal sayının toplamı 114 ise, bu sayıların en büyüğü kaçtır?
ÇÖZÜM:
1.sayı → x
2.sayı → (x + 2)
3.sayı → (x + 4)
Toplamları 114 olduğu için;
x + (x +2) + (x + 4) = 114
3x + 6 = 114
3x = 114 − 6
3x = 108
x = 36
En büyük sayı (x + 4) olduğu için;
36 + 4 = 40 olur.
Örnek:
Bir anne 36, kızı ise 12 yaşındadır. Kaç yıl sonra annenin yaşı kızının yaşının 2 katı olur?
ÇÖZÜM:
x yıl sonra anne (36 + x) yaşında,
x yıl sonra kızı (12 + x) yaşında olur.
x yıl sonra kızının yaşının 2 katı olduğu için;
(36 + x) = 2.(12 + x)
36 + x = 24 + 2x
36 − 24 = 2x − x
12 = x
Yüzde Problemleri:
Kar - Zarar Hesapları
Alış (maliyet) fiyatı= A
Satış (etiket) fiyatı= S
Kar oranı = K
Zarar oranı = Z
İndirim oranı = İ
1) Yüzde x kar ile satış
Satış fiyatı=Alış fiyatı + Kar
S=A+K ise S=A+[(A.x)/100]
2) Yüzde x zarar ile satış
Satış fiyatı=Alış fiyatı - Zarar
S=A-Z ise S=A-[(A.x)/100]
3) Yüzde x indirim ile satış
Satış fiyatı=Alış fiyatı -İndirim
S=A-İ ise S=A-[(A.x)/100]
Örnek:
120 TL’lik bir takım elbise yüzde 20 kar ile ne kadara satılır?
Önce kar oranını bulmalıyız.
120.(20/100) yani (120.20)/100 buradanda 2400/100
Kar=24 TL olur.
Satış fiyatı=Alış fiyatı + Kar
S=120+24=144 TL karlı satış
Örnek:
250 TL’lik bir cep telefonu yüzde 10 zarar ile ne kadara satılır?
Önce zarar oranını bulmalıyız.
250.(10/100) yani (250.10)/100 buradanda 2500/100
Zarar=25 TL olur.
Satış fiyatı=Alış fiyatı – Zarar
S=250-25=225 TL zararlı satış
Örnek:
600 TL’lik bir cep telefonu yüzde 20 indirim ile ne kadara satılır?
Önce indirim oranını bulmalıyız.
600.(20/100) yani (600.20)/100 buradanda 12000/100
İndirim=120 TL olur.
Satış fiyatı=Alış fiyatı – İndirim
S=600-120=480 TL indirimli satış
Faiz Problemleri:
Örnek:
24 TL yüzde kaç faizle 10 aylığına bankaya yatırılırsa 12 TL faiz getirir?
F=12 TL
A=24 TL
t=10 ay
n=?
F==(A.n.t)/1200
12=(24.n.10)/1200 (1200 karşıya çarpım olarak geçer)
14400=240n buradan her iki tarafı 240’a bölersek
n=60 çıkar.yani yüzde 60’tır.
Örnek:
1000 TL yüzde 3 faizle 3 yıllığına bankaya yatırılıyor.3 yıl sonra bankadan paranın hepsi çekiliyor.Ne kadar para çekilmiştir?
A=1000 TL
t=3 yıl
n=3
F=?
F==(A.n.t)/100
F=(1000.3.3)/100
F=9000/100 her iki taraf 100’e bölünürse
F=90 TL faiz getirir.
Bankadan 1000+90=1090 TL çekilir.Tamsayı Problemleri:
Kesir Problemleri:
O halde kitabın tamamı : 30 . 4 = 120 sayfadır.
Rasyonel Sayı Problemleri:Soru: 1Bir çalışan maaşını 1/5'ini ev kirasına, 1/3'ünü mutfak giderlerine, kalan maaşını 1/3'ünüde fatura giderine ayırıyor.
Bu çalışanın giderlerden sonra 560 lirası kaldığına göre, maaşı kaç liradır?
Çözüm:1/5 ile 1/3'ü toplayalım. Toplam maaşın tamamından çıkarark 1/3'ünü bulalum.
Maaştan kalan 560 lirayı kalan miktarın kesrine bölecez.
Kira ve mutfak giderleri:
1/5 + 1/3 = 3 +5 / 15 = 8/15 (payda eşitledik)
Kalan : 15 / 15 - 8 / 15 = 7/15 kalan parası
kalanın 1/3 ü ile fatura ödemişt.
7/15 'in 1/3 ünü bulalum:
7/15 . 1/3 = 7/45 olur.
Bu çalışanın toplam giderleri:
8/15 + 7/45 = 24+7/45 = 31/45
Tüm parasından çıkarırsak:
45/45 - 31/45 = 14/45
Giderlerden sonra 560 lirası kalıyordu.
Yani 14/45'i 560 olan sayıyı (x olsun) bulacağız.
14/45 . x = 560
x = 560 . 45 / 14
x = 1800 lira
Soru 2:
Soru 3:
Soru 4:
Soru 5:Bir işi Ahmet tek başına 12 günde, Mehmet tek başına 18 günde biitiriyor.
İkisi birlikte 1 gün çalışarak işin kaçta kaçını yaparlar?
Çözüm:İşin tamamını 12 günde bitiren Ahmet :
1 günde bu işin 1/12 sini bitirir.
işin tamamını 18 günde bitiren Mehmet:
1 günde bu işin 1/18'ini bitirir.
İkisi birlikte 1 günde işin kaçta kaçını bitireceklerini bulmak için
1/12 ile 1/18 ’i toplayalım.
1/12 + 1/18 = 3 + 2 / 36 = 5/36
İkisi birlikte 1 gün çalışarak işin 5/36 ’sını bitirebilirler.
Soru 6:Yüzey alanı 625 m kare olan yüzme havuzu, 1/25 m karelik karolarla kaplanıyor.
Bu iş için kaç tane karo kullanılır?
Çözüm:Kaç tane karo kullanıldığını bulmak için, havuzun yüzey alanını bir karonun yüzey alanına bölelim.
625 : 1/25 = 15 625
Havuzun yüzeyi için 15 625 tane karo kullanılmıştır
Soru 7:Bir tarlanın 1/2 ’sine buğday ekildikten sonra, kalan kısmın 1/3 ’üne arpa ekiliyor.
Arpa ekili alan 900 m2 olduğuna göre tarlanın tamamını bulalım.
Çözüm:1 tarlanın 1/2 ’sine buğday ekilmiştir.
Geriye tarlanın
1 - 1/2 = 2/2 - 1/2 = 1/2 'si kaldı.
kalanın 1/2'sinin 1/3'ü :
1/2 . 1/3 = 1/6 olur.
Arpa ekili alan tarlanın 1/6' sidr.
1/6'sı 900 olan tarlanın tamamı :
x. 1/6 = 900
x= 900.6 = 5400 m kare bululunur.
Soru 8:Merve’nin evi ile Zeynep’in evinin arası 95 tam 1/3 m’dir. Merve’nin bir adımı 13/27 m olduğuna göre
Merve’nin, kendi evinden Zeynep’in evine kaç adımda gidebileceğini bulalım.
Soru: 9
Soru 10:
Soru 11:Bir öğrenci 60 sayfalık bir kitabın önce 3/5'ünü sonrada 20 sayfasını okuyor.
Geriye okunmamış kaç sayfa kalmıştır?
ÇÖZÜM:60 syfaın 3/5'ünü bulalım:
60 . 3/5 = 36 sayfa
60 - 36 = 24 sayfa kaldı. Daha sonra 20 sayfa daha okumuş:
24 - 20 = 4 sayfa kalmış olur.
Bir Bilinmeyenli Denklem ProblemleriSoru 1 :Ayşe ile ablasının cevizlerinin toplamı 86’dır. Ayşe’nin cevizlerinin 2 katının 13 fazlası, ablasının cevizlerinin 3 katına eşittir. Her birinin kaçar cevizi vardır? Çözüm kümesi nedir?
Çözüm:Ayşe : X
Ablası : 86 - X
(Ayşe’nin cevizlerinin 2 katının 13 fazlası ) 2 . X + 13 = (86 - X ) . 3 (ablasının cevizlerinin 3 katına eşit)
2x + 13 = 258 - 3x
5x = 258 - 13
5x = 245
x = 49 (Ayşenin cevizi)
Ablasının Cevizi : 86 - 49 = 37
Ç = {49 , 37}
Soru 2:Bir araç satış galerisinde 75 araç vardır. İlk hafta 1/5'i , ikinci hafta 1/3'ü satılıyor.
Bu iki hafta sonunda galeride satılmayan kaç araç kalmıştır?
Çözüm:75 araç var. İlk hafta 1/5 i satılırsa;
75. 1/5= 15 araç satılır demektir. ( ilk hafta 15 araç satıldı)
ikinci hafta 1/3 ü satılırsa;
75. 1/3 = 25 araç satılır. ( ikinci hafta 23 araç satılmış)
15 + 23 = 38 (toplamda satılan araç)
75 araç vardı 38 araç satıldı. Kaç araç geriye kalır?
75 - 38=37 (kalan araç sayısı)
Soru 3:Yedi katının sekiz fazlası 71 olan sayıyı bulunuz? (Denklem kurarak)
Çözüm:Bu bilinmeyen sayımız X olsun.
Bu sayının 7 Katı : 7.X
Bu sayının 7 katının 8 fazlası : 7.X + 8 Bu sayı 71'e eşit olacak.
7.x + 8 = 71 olur.
7.X = 71 - 8 ( 8 sayısı eşitliğin karsısına işaret değiştirerek geçti)
7.X = 63 (X'i yalnız bırakmak için her iki tarafı 7'ye bölersek)
X = 9
Soru 4:Bir sınıftaki öğrenciler üçerli otururlarsa 5 öğrenci ayakta kalıyor.
Dörderli otururlarsa 1 sıra boş kalıyor.Bu sınıfın mevcudu kaçtır?
Çözüm:Sıra sayısı: X olsun
Üçerli oturup 5 öğrenci ayakta kalıyorsa : 3.X + 5 olur.
Dörderli oturup 1 sıra boş kalıyorsa: 4(X-1) Denkelmi eşitlersek:
3.X + 5 = 4.(X - 1 )
3.X + 5 = 4 . X - 4
5 + 4 = 4X - 3X
9 = X (Bu sınıfta 9 sıra varmış)
İki denklemden herhangi birine yazarak sınıf mevcudunu buluyoruz..
3.x + 5 denkleminde x yerine 9 yazarsak:
3 . 9 + 5 = 32 (sınıf mevcudu)
Soru 5:Bir satıcının elinde bulunan 20 çift çorabın, bir kısmının çifti 3 lira, diğerlerinin çifti 5 liradır.
Satıcını elindeki çorapların toplam değeri 76 lira oldğuna göre;
3 liralık kaç çift çorabı bulunmaltadır?
Çözüm:3 liralık çorabı : X tane olsun.
5 liralık çorabı : 20 - X tane olur.
3. x + 5. (20 - x) = 76 (Satıcını elindeki çorapların toplam değeri 76 lira)
3.x + 100 - 5.x = 76
100 - 76 = 5.x - 3.x
24 = 2x
12 = x (3 liralık çorap sayısı)
Soru 6:Sezgin sınıf listesinde baştan (n+5). sırada, sondan (3n-2). sıradadır.
Sınıf mevcudu 42 kişi olduğuna göre; Sezgin baştan kaçıncı kişidir?
Çözüm:Önündeki ve arkasındaki kişilerin toplamı sınıf mevcudu olur.
Yalnız İki kez saymamak için 1 ile çıkarmayı unutmayalım.
(n+5) + (3n -2) - 1 = 42
n + 5 + 3.n - 2 - 1 = 42
4.n + 5 - 3 =42
4.n = 42 - 2
4.n = 40
n = 10
Baştan (n+5) = 10 + 5 = 15. kişidir.
Soru 7:
Soru 8:3x + 4 = 16 denklemindeki x bilinmeyenini sayma pulları ile modelleyerek bulalım.
Çözüm: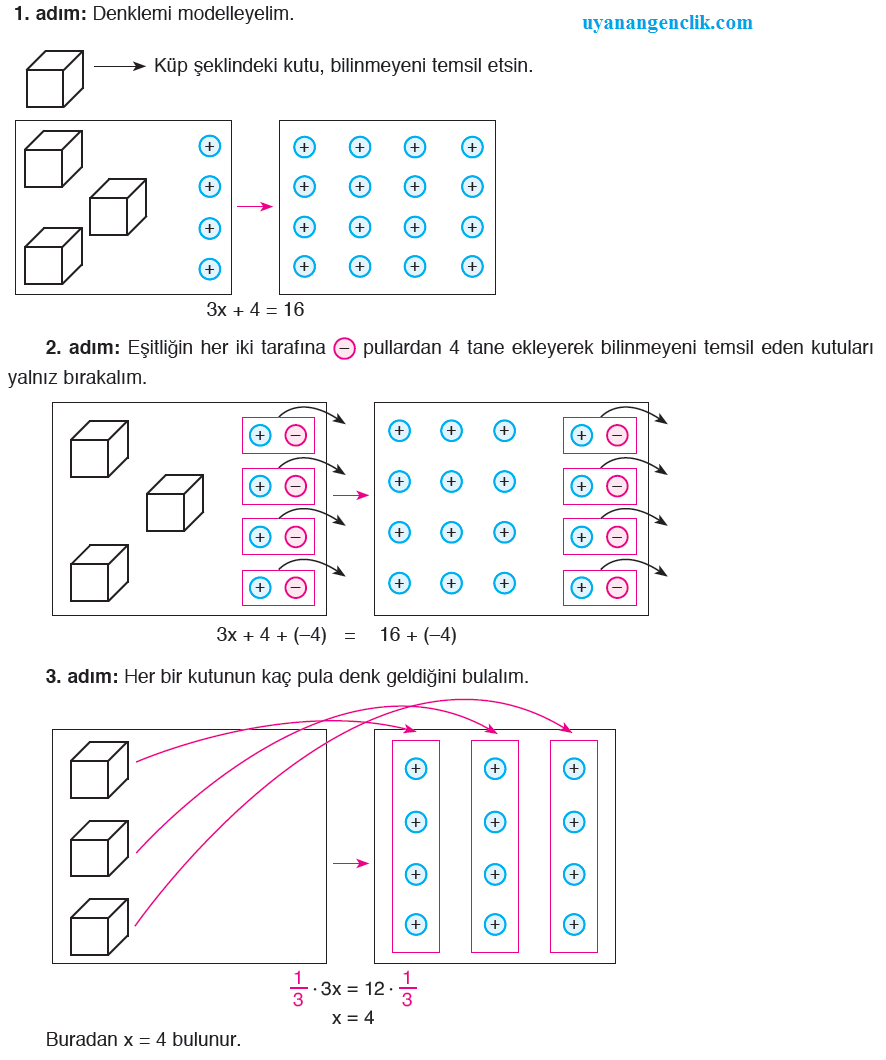
Soru 9:
Soru 10:
Soru 11:Meltem Hanım, marketten tanesi 50 kr. ve 1 TL’lik çikolatalardan toplam 36 tane alarak 26 TL ödüyor.
Meltem Hanım’ın 1 TL’lik çikolatalardan kaç tane aldığını bulalım.
Çözüm:Tanesi 1 TL olan çikolataların sayısı x ile ifade edilirse tanesi 50 kr. olan çikolataların sayısı 36 – x
olur.
Tanesi 1 TL olan çikolataların tamamı için ödenen para, 1 TL = 100 kr. olduğundan
100 · x’tir. ...(1)
Tanesi 50 kr. olan çikolataların tamamı için ödenen para,
50 · (36 – x)’tir. ...(2)
Alınan çikolatalara ödenen toplam para 26 TL = 2600 kr. olduğundan, (1) ve (2) denklemlerini toplayacağız
ve 2600’e eşitleyeceğiz.
100 · x + 50 · (36 – x) = 2600 olur. ...(3)
(3) denklemini çözersek 1 TL’lik çikolataların sayısını bulmuş olacağız.
100 · x + 50 · (36 – x) = 2600
100x + 50 · 36 – 50x = 2600
50x + 1800 = 2600
50x = 2600 – 1800
50x = 800
x = 800/50
x = 16’dır.
1 TL’lik çikolataların sayısı 16 olarak bulunur.
Soru 12:Bir otobüsteki erkeklerin sayısı, kadınların sayısının 2 katıdır.
Bu otobüsten 6 evli çift inince, erkeklerin sayısı kadınların sayısının 3 katı oluyor.
Başlangıçta otobüsteki yolcu sayısını bulalım.
Çözüm:Otobüsteki kadınların sayısına x diyelim.
Erkeklerin sayısı: 2x olur.
6 evli çift inince:
x – 6 (kadın) 2x – 6 (erkek olur.)
Son durumda erkeklerin sayısı kadınların sayısının 3 katı olduğuna göre
3 · (x – 6) = 2x – 6 denklemini yazarız. Bu denklemi çözelim.
3 · (x – 6) = 2x – 6
3x – 18 = 2x – 6
3x – 2x = –6 + 18
x = 12 (Başlangıçta otobüsteki kadınların sayısı) olur.
Başlangıçta otobüsteki erkeklerin sayısı 2x = 2 · 12 = 24’tür.
Sonuç olarak başlangıçta otobüsteki yolcu sayısı, 12 + 24 = 36 olarak bulunur.
Soru 13:Eray’ın yaşı, Gül’ün yaşının 6 katıdır. 2 yıl sonra ikisinin yaşları toplamı 32 olduğuna göre Eray’ın
bugünkü yaşını bulalım.
Çözüm:
Soru 14:
Soru 15:Hangi sayının 3 eksiğinin 2 katının, aynı sayının 4 fazlasına eşit olduğunu bulalım.
ÇÖZÜMBilinmeyen sayıya x diyelim ve verilen probleme ait denklemi kuralım.
(x – 3) · 2 = x + 4
2x – 6 = x + 4
2x – x = 4 + 6
x = 10 bulunur.
Soru 16:Bir sınıfta 29 öğrenci ve 12 sıra vardır. Öğrencilerin bir kısmı sıralara ikişer ikişer, bir kısmı üçer
üçer oturduğunda, hiç kimse ayakta kalmıyor. Buna göre öğrencilerin ikişer ikişer oturduğu sıra sayısı
kaçtır?
ÇÖZÜM:2 şerli sıra sayısı : x
3'erli sıra sayısı : 12 - x olur.
2. x + 3 (12 - x) = 29
2x + 36 - 3x = 29
36 - 29 = x
7 = x
ik şer ikişer " " " = 7
Üçer üçer oturulan sıra sayısı = 5
Sağlaması:
3 . 5=15
2 . 7=14 buradan toplam 29 öğrenci olur.
Soru: 17Bir otelde tek yataklı ve çift yataklı odalar vardır. Oteldeki toplam yatak sayısı 160’tır.
120 odalı bu otelde kaç tane çift kişilik oda vardır?
ÇÖZÜM:Çift kişilik oda sayısı : X olsun
Tek kişilik oda sayısı : 120 - X
2.x + 1.(120-x) = 160
2x +120 - x = 160
x = 160 - 120 = 40 tane çift kişilik oda vardır.
Soru 18:Sibel, kitapçıdan 5 adet hikâye kitabı alıyor. Kitaplar 3 lira daha ucuz olsaydı, 2 kitap daha alabilecekti.
Sibel’in aldığı bir kitabın fiyatı kaç liradır?
ÇÖZÜM:
Kitabının fiyatına : x diyelim.
x . 5 = 7 . ( x - 3)
5x = 7x - 21
2x = 21
x = 10,5 lira
27 Yanıt
20139 Gösterim